II.3 Corps des modules

II.3.1 Action de Galois

a. Corps de définition

Soit K un corps de nombres. On dit qu'un dessin est défini sur K s'il peut être représenté par un couple (X, ) où est une fonction de X définie sur K. Pour un dessin marqué, nous demandons que la face marquée soit définie sur K.

Remarquer que les automorphismes du dessin (s'il y en a) ne sont pas nécessairement définis sur K. Par exemple x x³.

b. Corps des modules 

Le groupe Gal( / Q) agit sur les dessins (revêtements). On peut voir cela comme son action sur les coefficients des équations de n'importe quelle paire de Belyi. On va appeler _D le stabilisateur d'un dessin D. Le corps K_D des modules du dessin est le corps fixé par _D.

Coombes et Harbater [14] ont prouvé que le corps des modules est l'intersection de tous les corps de définition.

Couveignes [16] a montré qu'il existe des dessins pour lesquels le corps des modules n'est pas un corps de définition et qu'en genre 0, tout dessin admet un modèle sur une extension au plus quadratique de son corps des modules. En genre 0, le corps des modules est toujours corps de définition d'un dessin marqué.

c. Caractéristiques du corps des modules

Par définition, le degré du corps des modules est égal au nombre de dessins dans l'orbite sous l'action de Gal( / Q). Son discriminant est nettement plus mystérieux, on se demande par exemple quels nombres premiers en sont des diviseurs.

Beckmann [4] a prouvé (dans un cadre plus général) que les facteurs premiers du discriminant sont des diviseurs de l'ordre du groupe de monodromie. La réciproque est bien évidemment fausse, mais on ne connait pas de caractérisation combinatoire qui réponde à cette question.

d. L'action de Galois est fidèle

Le groupe Gal( / Q) agit fidèlement sur les dessins. Cela signifie que pour tout élément , on peut construire un dessin sur lequel agit non trivialement. En d'autres termes, tout corps de nombres est le corps des modules d'un dessin.

Plus précisément, le groupe Gal( / Q) agit fidèlement sur les dessins de genre 1. De plus, H.W. Lenstra a prouvé que l'action de Gal( / Q) est fidèle sur les arbres (cf. [37, pp56-59]).

Cette propriété permet d'étudier Gal( / Q) en étudiant les dessins d'enfants, en particulier les arbres. L'action de Gal( / Q) sur les dessins se compare à son action sur le corps des modules du dessin.

II.3.2 Invariants galoisiens

a. Orbites sous l'action de Galois

Pour l'étude de l'action de Gal( / Q) sur les dessins, il est important de savoir déterminer si deux dessins sont conjugués. L'idéal serait de pouvoir n'utiliser que la définition combinatoire des dessins pour établir un critère décidant de l'appartenance ou non à la même orbite. On connait quelques invariants combinatoires pour séparer deux orbites, mais la seule méthode sûre est de calculer les fonctions de Belyi des dessins.

b. Liste des valences

Nous allons introduire une notation pour la liste des valences d'un dessin, qui ressemble à la notation employée par Malle [29]. Si a_n (resp. b_n , c_n ) est le nombre de zéros (resp. uns, faces) de valence n, le symbole

[n^c_n... 2^c₂1^c₁; n^a_n... 1^a₁; n^b_n... 1^b₁]

représente l'ensemble des dessins ayant mêmes valences. Bien évidemment, on omettra les valences absentes et les exposants 1. Par exemple, le ``petit bonhomme'' de la figure II.5 a pour liste de valences [7 1; 4 2 1²; 3³ 1²]. Pour un dessin marqué, on placera en premier la face marquée.

L'action de Galois sur une fonction de Belyi ne modifie par la structure de la ramification. Deux dessins conjugués par l'action de Galois ont donc même liste de valences, mais la réciproque est fausse. La liste des valences est un invariant galoisien qui ne suffit pas à séparer les orbites.

On peut raffiner cet invariant en remarquant que si la monodromie d'un dessin est le triplet (₀, ₁, ), alors l'action de Galois sur les dessins induit une action de Inn(G) sur ces triplets.

c. Composition de dessins

Si un dessin est une composition de revêtements (voir II.3.3.b. pour plus de détails sur la composition de dessins), le groupe de Galois absolu agit sur chaque étage de la tour de revêtements. Nous avons ainsi un deuxième invariant galoisien. Par exemple, l'orbite galoisienne d'un dessin qui est un k-multiple ne contient donc que des k-multiples. L'invariant (ordre abélien) introduit par Pakovitch [36] est un autre cas particulier.

Ces deux critères combinatoires suffisent vraisemblablement à séparer les arbres en Y (cf. § IV.3.1).

d. Les fleurs de Leila

On connait des exemples, en particulier les ``Fleurs de Leila'', pour lesquels un critère supplémentaire est nécessaire. Cet invariant a été formalisé par Zapponi [49] d'après un travail expérimental de Kochetkov, et correspond à la signature d'une permutation.

 
Figure II.12: Fleurs de Leila

II.3.3 Morphismes de dessins 

a. Automorphismes d'un dessin

Certains dessins ont une certaine symétrie, qui correspond à un automorphisme du revêtement. Du point de vue de P7 un automorphisme du dessin est une permutation qui commute avec ₀ et ₁ (donc aussi avec ), c'est-à-dire un élément du centralisateur du groupe de monodromie dans _N.

Si le dessin a des automorphismes, leur étude préalable simplifie beaucoup l'étude du dessin.

b. Composition de dessins 

Nous cherchons à contruire un dessin à partir de dessins plus petits. Supposons que nous avons trois surfaces (ou courbes algébriques) X, Y et Z et deux revêtements ramifiés D : X Y et D : Y Z. La composition D o D est le revêtement X ^o Z.

Lorsque ces trois revêtements sont des dessins d'enfants, nous parlons de ``composition de dessins''. C'est le cas si Y = Z = P₁ et si ({0, 1, }) est inclus dans {0, 1, }. Nous appelons dessin gelé un dessin de genre 0 dont nous avons fixé la fonction de Belyi de telle sorte que les éléments 0, 1, soient des points de type , ou . Nous pouvons, sans perte de généralité, supposer que est une face, et nous représentons les dessins gelés en traçant un carré autour des valeurs 0 et 1. La figure II.13 donne deux exemples de composition par un dessin gelé.

 
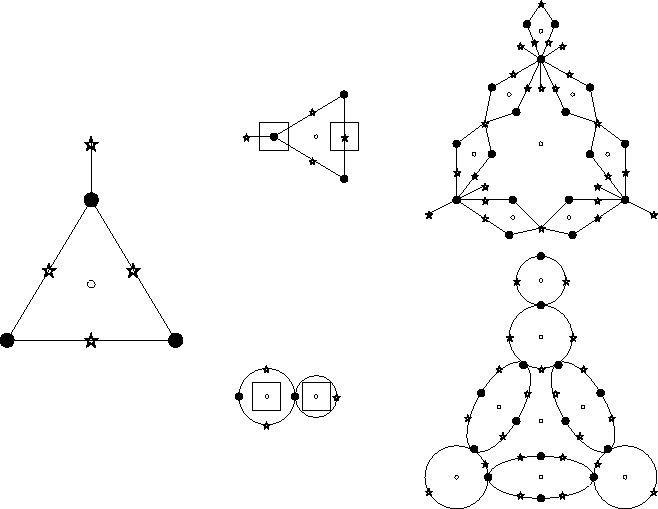
Figure II.13: Exemples de composition de dessins

On peut généraliser ceci au cas où D : est un revêtement fini (mais pas un dessin) X P₁ ramifié au dessus d'un ensemble R tel que (R) soit inclus dans {0, 1, }. C'est ce qui est utilisé par Birch pour obtenir quelques exemples en genre 1 (cf. § III.2.1.a.).

c. Double, ou foncteur de Walsh 

Nous avons défini C₂⁺ comme sous-groupe d'index 2 de H₂⁺, ce qui définit les dessins propres comme des cas particuliers de dessins d'enfants. On peut aussi regarder l'inclusion de H₂⁺ = (2) dans C₂⁺ = ₀(2). Cela permet d'associer à tout dessin un dessin propre, que nous appelons son double.

 
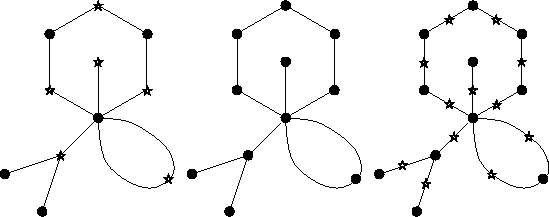
Figure II.14: Doublement d'un dessin.

Cette construction se fait en oubliant le type des sommets d'une carte bipartite, comme sur la figure II.14. C'est la composition par le dessin gelé de la figure ci-dessous, c'est à dire par la fonction : 4 (1 - ).

On voit donc que le calcul de la fonction de Belyi d'un dessin propre (de degré 2n) qui est le double d'un autre dessin se réduit au calcul d'une fonction de Belyi de degré n. On verra (paragraphe III.1.2.d.) que le calcul d'une fonction de Belyi se simplifie aussi pour les dessins propres qui ne sont pas des doubles.

d. Autres foncteurs

L'inclusion de C₂⁺ = ₀(2) dans T₂⁺ = (1) transforme un dessin propre en une triangulation à l'aide de : 27² / (4 - )³. Tout ceci est développé en détail par Jones et Singerman [26, §7] ; c'est aussi un cas particulier de composition de dessins.

e. Autres multiples

Si on décompose chaque segment de la carte en k segments, on obtient un multiple du dessin. On peut remarquer que la factorisation de k permet de construire la k-multiplication comme une tour de revêtements.

Comme on le verra en IV.2.2, le polynôme  _k pour le k-ième multiple est la composition ^-1 o T_k o où T_k est le k-ième polynôme de Tchebitchev et (x) = 1 - 2x. Le triple est donc par exemple la composition par : (4-3)². Le quintuple est la composition par : - (16² + 20+5)².

 
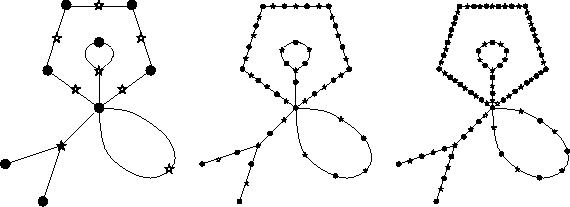
Figure II.15: Dessin, triple et quintuple

II.3.4 Énumération des dessins 

a. Dessins réguliers et semi-réguliers

En genre 0, tous les dessins semi-réguliers sont galoisiens, et il est possible d'en donner la liste complète. Ce sont les dessins en étoile, de liste de valences [n; n; 1ⁿ], les cercles, de liste de valences [n¹; 2ⁿ; 2ⁿ], et les solides réguliers : tétraèdre [3⁴; 3⁴; 2⁶], cube ou octaèdre [4⁶; 3⁸; 2¹²] et dodécaèdre ou icosaèdre [5¹²; 3²⁰; 2³⁰].

En genre 1, ce sont les quotients des réseaux réguliers carré ou triangulaire, sur les courbes j=0 et j=1728. En genre supérieur à 1, la formule de Riemann-Hurwitz donne une majoration de l'ordre du groupe de symétrie du dessin (84(g-1)) ; Adrinanov et Shabat [1] détaillent le sujet.

b. Arbres

Une formule d'énumération remontant apparemment à Tutte [46] s'applique aux dessins n'ayant qu'une face. On note ##[L] le nombre de dessins ayant pour liste de valence [L], en comptant avec un poids 1/k les dessins ayant k automorphismes. Pour un arbre de liste de valences [d ; p₁^a₁... p_m^a_m ; q₁^b₁... q_n^b_n],

##[L]  =  (a₁+a₂+...+a_m-1)! / a₁!a₂!...a_m!  ×  (b₁+b₂+...+b_n-1)! / b₁!b₂!...b_n!

Cette formule donne facilement un majorant de la longueur de l'orbite du dessin sous l'action de Galois. Le paragraphe suivant donne une majoration plus précise.

c. Classes de conjugaison 

À partir de la présentation P7 pour les dessins, nous posons G _d le groupe engendré par < ₀, ₁, >, qui est donc un groupe de permutations transitif sur d lettres. Nous nous intéressons aux classes de conjugaison c_i de ₀, ₁ et dans G.

Nous supposerons que ces classes de conjugaison sont rationnelles, c'est-à-dire que c_i* = c_i, ce qui signifie que (c_i) est dans Q. La longueur de l'orbite du dessin sous l'action de Galois est au plus le nombre n_C ci-dessous, pour k=3. Cette majoration est issue de la théorie de la rigidité et on la trouve chez Matzat [33] ou Serre [41, p68] (démontrée pour le cas où G n'a pas de centre). D'autres majorations, parfois plus fines, peuvent être construites de façon similaire.

n_C = |Z(G)| |G|^-2 |c₁|...|c_k|   (c₁)...(c_k) / (1)^k-2.

II.3.5 Rigidité 

a. Motivation

La théorie de Galois, que nous avons évoquée au paragraphe I.1.2.c. pour les corps de nombres, se généralise aux extensions de corps de fonctions et aux revêtements algébriques. On cherche à résoudre le problème de Galois inverse sur Q, c'est-à-dire qu'on veut prouver que tout groupe fini est groupe de Galois sur Q. Ce problème est ouvert, mais il est possible d'en résoudre des cas particuliers en construisant des dessins d'enfants définis sur Q et de groupe de monodromie choisi. À partir de ce dessin, on calcule une extension (régulière) de Q(T) de même groupe de Galois, dont on déduit la propriété inverse de Galois sur Q.

Nous aurons donc besoin de savoir, lorsque nous avons la description combinatoire d'un dessin, s'il est défini sur Q. Une méthode est le calcul explicite de sa fonction de Belyi, mais il y a souvent plus rapide.

La borne sur la taille de l'orbite de Galois, donnée au paragraphe II.3.4.c., nous donne un critère de rationalité (n_C = 1), qui est un cas particulier du critère de rigidité donné par Serre [41] (voir le théorème 2 ci-dessous) qui est lui-même un cas particulier des critères plus généraux exposés par Matzat ([33], avec démonstrations dans son livre [32]) dont nous donnons un aperçu avec le théorème 3.

La rigidité, et la non rigidité, ont été un candidat pour une résolution générale du problème de Galois inverse sur Q, et ces théories ont connu des nombreux développements. On peut notamment remarquer que si nous nous limitons dans cette thèse aux dessins d'enfants (et éventuellement aux revêtements de P₁ ramifiés au dessus de k>3 points), la théorie s'est étendue aux revêtements de surfaces (compactes orientées) de genre g ramifiés au dessus de k points et aux corps de fonctions à s variables.

b. Passage de P₁ (revêtements) à Q (corps de nombres)

Une correspondance très riche entre revêtements et extensions donne la technique pour construire des extensions (régulières) de corps de fonctions de groupe de Galois fixé, à partir d'un revêtement dont on connait le groupe de Galois a priori.

Soit L une extension finie du corps Q(T) des fractions rationnelles sur Q. On dit que cette extension est régulière si L = Q, ce qui signifie que le produit tensoriel de L et est une extension finie de (T) ayant la même structure. La régularité d'une extension permet d'avoir un parallèle entre l'aspect arithmétique (sur Q) et l'aspect géométrique (sur ou C).

Si : XP₁ est un revêtement de courbes algébriques sur Q, le corps Q(X) des fonctions rationnelles sur X est une extension régulière de Q(T). Réciproquement, si L est une extension finie régulière de Q(T), alors c'est le corps des fonctions d'une courbe projective lisse X. L'inclusion Q(T) L définit un revêtement X P₁. Si l'extension L / Q(T) est galoisienne de groupe G, alors le revêtement correspondant est galoisien de groupe G.

Le théorème d'irréducibilité de Hilbert permet de transférer cette construction de Q(T) à Q. En effet, si f(T, X) élément de Q(T)[X] est un polynôme irréductible sur Q(T), il existe une infinité de spécialisations de la variable T, c'est-à-dire d'éléments t de Q tels que le groupe de Galois sur Q de f(t, X) élément de Q[X] soit égal au groupe de Galois de f sur Q(T).

c. Classification de Hurwitz

Nous posons = { (g₁ , ... , g_k) éléments de G^k , tels que g₁ ... g_k = 1 } et son sous-ensemble des k-uplets engendrant le groupe G.

Si nous fixons k places de C(T)  (c'est-à-dire k valeurs de ramification dans P₁C) alors l'ensemble ^a = / Aut(G) des orbites de modulo les automorphismes de G classifie bijectivement les revêtements de C(T) de groupe de Galois G ramifiés au dessus de ces k points. C'est ce qu'on appelle la classification de Hurwitz.

Le problème de Galois sur C(T), et par la même sur (T), est ainsi résolu puisqu'il existe des k-dessins de groupe G, pour tout groupe fini. Le problème de rationalité de ces k-dessins est la question de savoir s'ils sont définis sur Q, ou de connaitre un corps de définition assez petit.

On considère k classes de conjugaisons c₁, ... ,c_k , non nécessairement distinctes. On note C = {(g₁,...,g_k) dans G^k tels que g_i soit dans c_i} qu'on appelle une structure de classes de G et C* = {(g₁,...,g_k) dans G^k tels que g_i soit dans c_i*} qu'on appelle une structure de ramification.

L'action de Gal( / Q) sur les revêtements conserve la structure de ramification. Nous pouvons donc étudier la restriction de la classification de Hurwitz à une certaine structure de ramification. Si cette restriction ne contient qu'un élément (modulo les automorphismes de G) alors l'orbite du revêtement sous Gal( / Q) est réduite à un élément. C'est le critère de rigidité. La réciproque est fausse, et il existe d'autres critères (voir en particulier [33]).

d. Constantes de structure

On note comme Matzat C° qui vaut indifféremment C ou C*. Nous définissons les quatre ensembles _C° = { (g₁ , ... , g_k) éléments de C° , tels que g₁ ... g_k = 1 } et _C° = { (g₁ , ... , g_k) éléments de _C° , tels que < g₁ , ... , g_k > = G }. Sur ces ensembles opèrent les groupes Inn(G) des automorphismes intérieurs de G et Aut_C°(G) des automorphismes conservant la structure de classes (ou de ramification).

Les objets qui nous intéressent sont les quotients ^a_C° = _C° / Aut_C°(G) et ⁱ_C° = _C° / Inn(G). En particulier, ^a_C* énumère les revêtements ayant une structure de ramification donnée. Ces ensembles sont finis, et leurs cardinaux sont les nombres entiers l ⁱ_C = | ⁱ_C| et autres. Nous devons aussi définir le nombre n_C° = |_C° / Inn(G)|, qui est intervenu au paragraphe II.3.4.c. et que Matzat appelle constante de structure normalisée.

Ces entiers sont liés par les égalités l ⁱ_C* = e_C l ⁱ_C (l'entier e_C est appelé indice cyclotomique) l ⁱ_C° = a_C° l ^a_C° (l'entier a_C° est égal au cardinal de Out_C°(G) = Aut_C°(G) / Inn(G), ensemble des classes d'automorphismes extérieurs) et nous avons l'inégalité l ⁱ_C°n_C° à cause de l'inclusion .

On voit donc que n_C*l ⁱ_C*l ^a_C* sont des majorants du nombre de conjugués galoisiens du dessin.

e. Rationalité et rigidité 

Il n'est pas nécessaire de calculer toutes ces constantes. On dit qu'une classe c dans Cl(G) est K-rationnelle si l'image de c par les caractères irréductibles de X(G) est toujours dans K. Il est équivalent de dire que cⁿ = c pour tout _n dans Gal( K(_N) / K). En particulier, puisque Q^ab (on note ainsi l'extension abélienne maximale de Q, parfois aussi notée Q^cycl car c'est l'extension cyclotomique maximale) contient tous les _N, toute classe de conjugaison est Q^ab-rationnelle. La Q-rationalité de c est équivalente à l'égalité c* = c.

On dit qu'un k-uplet C de classes de conjugaisons est rigide si l ⁱ_C = 1 et qu'il est strictement rigide si de plus _C = _C. Dans le cas où G n'a pas de centre, la condition de rigidité devient |_C| = |G| (Serre [41, p70]).

Théorème 2 (D'après Serre)
Soit G un groupe fini de centre trivial. Si le k-uplet (c₁,...,c_k) de classes de conjugaisons de G est rigide et si toutes les c_i sont K-rationnelles, alors il existe une extension régulière de K(T) de groupe de Galois G. Cette extension correspond à un revêtement de P₁ défini sur K non ramifié hors d'un ensemble {p₁,...,p_k} de points K-rationnels et dont la monodromie en p_i est engendrée par un élément de c_i.

Ce revêtement est unique à G-isomorphisme près si on fixe les points p_i et si on choisit une racine primitive N-ième de l'unité dans K, c'est-à-dire un facteur du polynôme cyclotomique dans K.

Si k=3 et {p_i} = {0, 1, }, nous avons un dessin d'enfant. Le calcul de la correspondance de Grothendieck permet alors d'expliciter l'extension L / K(T). Bien évidemment, ceci est surtout intéressant si K = Q, mais les conditions sur le k-uplet (c₁, ..., c_k) sont trop sévères pour être souvent vérifiées. Serre [41, p84] cite une variante simple du théorème 2 où la Q-rationalité de toutes les c_i n'est pas nécessaire pour avoir une extension de Q(T).

f. Un critère de rationalité

D'un point de vue bien plus général, nous pouvons avoir une version du théorème 2 où toutes les hypothèses sont affaiblies.

Le centre Z(G) du groupe G ne doit pas nécessairement être trivial. Il suffit que Z(G) ait un complément dans G. Cela signifie qu'il existe un sous-groupe H tel que tout élément g de G se factorise de façon unique en un produit uh où u est élément de Z(G) et h de H.

L'hypothèse de rigidité est en fait une hypothèse sur la valeur de n_C. L'hypothèse de rationalité peut être généralisée en calculant l'entier e_C.

Théorème 3 (D'après Matzat)
Si le centre de G a un complément si l ⁱ_C > 0, il existe une extension régulière de K(T) de groupe de Galois G et de structure de ramification C*.
L'intersection K₀ de K avec le corps engendré par les valeurs des caractères irréductibles sur les classes de C est un corps abélien tel que [K : K₀] l ⁱ_C et [K₀ : Q] e_C.

Si C est rigide, nous retrouvons le résultat de Serre : K = Q lorsque e_C = 1, donc lorsque le k-uplet C est invariant par élévation aux puissances n-ièmes, c'est-à-dire si les caractères sont globalement invariants sous l'action du groupe Gal( / Q).

Il existe d'autres critères de rationalité, utilisant par exemple l'action du groupe de tresses sur le lieu de ramification.