II.2 Double visage combinatoire - géométrie
II.2.1 Aspect combinatoire
Nous donnons sept présentations équivalentes
des dessins d'enfants,
qu'il est utile de combiner pour en percevoir les
applications.
L'équivalence entre ces descriptions est
classique et date de bien avant l'étude
des dessins d'enfants. Nous n'en ferons
donc pas des démonstrations complètes.
a. Topologie
Présentation 1
(Carte bipartite)
Une carte (S, K, X)
est bipartite si elle est munie d'une application
S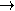 {
{ ,
,
 }
donnant un type aux sommets, telle que chaque arête
soit adjacente à deux sommets de types
différents.
}
donnant un type aux sommets, telle que chaque arête
soit adjacente à deux sommets de types
différents.
La catégorie P1 a pour objets
les cartes bipartites sur une surface orientable
et les morphismes
sont les homéomorphismes conservant le type des sommets.
Ceci est la définition la plus visuelle,
celle qui permet de tracer effectivement
des dessins au sens commun du terme.
Pour encore plus de simplicité, nous
pouvons oublier le type
des sommets d'un dessin et obtenir
un dessin propre (cf. § II.2.2.b.).
Présentation 2
(Triangulations bicolorées)
Une triangulation (S, K, X)
est bicolorée si ses cellules (triangles) sont de deux couleurs
déterminées par une application X-K
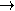 {±1}
telle que deux triangles adjacents sont de couleurs différentes.
{±1}
telle que deux triangles adjacents sont de couleurs différentes.
Nous pouvons remarquer que si une surface compacte X
est munie d'une triangulation bicolorée,
elle est orientable.
On aborde parfois le sujet des dessins d'enfants
par l'étude des triangulations
[3].
Présentation 3
(Triangulations tripartites)
Une triangulation (S, K, X)
tripartite si elle est munie d'une application
S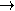 {
{ ,
,
 ,
,
 }
donnant un type aux sommets, telle que chaque arête
soit adjacente à deux sommets de types
différents.
}
donnant un type aux sommets, telle que chaque arête
soit adjacente à deux sommets de types
différents.
Ces deux dernières présentations sont équivalentes.
Si nous avons une triangulation tripartite,
chaque cellule a trois sommets de types distincts.
Pour chacune, l'ordre des sommets
 ,
,
 ,
,
 donne une orientation.
Lorsque nous avons choisi une orientation sur X,
cela nous donne une bicoloration des cellules.
donne une orientation.
Lorsque nous avons choisi une orientation sur X,
cela nous donne une bicoloration des cellules.
Réciproquement, soit une triangulation bicolorée.
Nous choisissons un sommet a qui sera de type
 et un sommet b adjacent à a qui sera de type
et un sommet b adjacent à a qui sera de type
 .
Ceci permet de construire de proche en proche
un partition des sommets telle que les trois sommets
d'un triangle soient de types différents.
À cause de la bicoloration, le nombre
de triangles adjacents à un sommet donné est pair,
cette construction est donc cohérente.
.
Ceci permet de construire de proche en proche
un partition des sommets telle que les trois sommets
d'un triangle soient de types différents.
À cause de la bicoloration, le nombre
de triangles adjacents à un sommet donné est pair,
cette construction est donc cohérente.
Nous pouvons construire une correspondance
entre la présentation P3
des dessins sous la forme de triangulations tripartites
et la présentation P1
sous la forme de cartes bipartites.
Prenons une triangulation tripartite (S,K,X).
Soit S' l'ensemble des sommets de type
 ou
ou
 ,
et soit K' la réunion des sommets de S'
et des arêtes reliant deux sommets de S'.
Alors (S',K',X) est une carte bipartite.
Il y a un point
,
et soit K' la réunion des sommets de S'
et des arêtes reliant deux sommets de S'.
Alors (S',K',X) est une carte bipartite.
Il y a un point
 dans chaque cellule,
et cette cellule est la réunion des triangles
touchant ce point.
dans chaque cellule,
et cette cellule est la réunion des triangles
touchant ce point.
Présentation 4
(Hypercartes)
Un dessin est aussi une classe d'homéomorphisme
d'hypercartes sur une surface connexe
compacte orientable.
Cette présentation est équivalente aux
précédentes.
En effet, si (S,K,X) est la carte
délimitant les cellules (de trois types)
d'une hypercarte P4, sa carte duale
est une triangulation tripartite P3.
Figure II.5: Le ``petit bonhomme'' :
carte bipartite, triangulation et hypercarte
(les flèches sont numérotées de 1 à 8).
b. Choix de terminologie
À cause des propriétés géométriques et algébriques
(voir P8), nous appellerons
zéro les points de type
 et un ceux de type
et un ceux de type
 .
Nous appellerons face les cellules,
ou bien les points
.
Nous appellerons face les cellules,
ou bien les points
 .
La description P3
sous la forme de triangulations
tripartites montre qu'il est facile
de permuter les rôles de ces trois
types de points.
.
La description P3
sous la forme de triangulations
tripartites montre qu'il est facile
de permuter les rôles de ces trois
types de points.
Nous appellerons flèche un segment reliant
un  et
un
et
un  (selon P1),
ou bien le triangle positif contigu
(selon P2)
ou le sommet positif correspondant
(selon P4).
(selon P1),
ou bien le triangle positif contigu
(selon P2)
ou le sommet positif correspondant
(selon P4).
 Nous appellerons triangle chaque cellule
de la triangulation (selon P2
ou P3).
Les triangles positifs correspondent aux demi-segments de
Nous appellerons triangle chaque cellule
de la triangulation (selon P2
ou P3).
Les triangles positifs correspondent aux demi-segments de
 vers
vers  et les triangles négatifs aux demi-segments de
et les triangles négatifs aux demi-segments de
 vers
vers  .
.
 Nous appellerons fléchette les six types de
demi-segments,
Nous appellerons fléchette les six types de
demi-segments,
 -
-
 ,
,
 -
-
 ,
,
 -
-
 ,
,
 -
-
 ,
,
 -
-
 ou
ou
 -
-
 .
.
 Nous évitons ainsi le terme de drapeau qui sert à
désigner parfois les flèches, parfois les triangles.
Le degré du dessin est le nombre de flèches.
C'est donc le nombre d'arêtes de la carte bipartite
(catégorie P1)
ou bien le nombre de triangles de chaque type
(P2).
Nous évitons ainsi le terme de drapeau qui sert à
désigner parfois les flèches, parfois les triangles.
Le degré du dessin est le nombre de flèches.
C'est donc le nombre d'arêtes de la carte bipartite
(catégorie P1)
ou bien le nombre de triangles de chaque type
(P2).
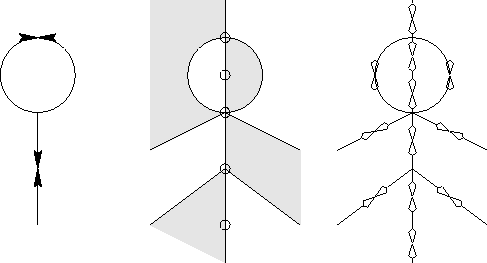
Figure II.6: Flèches, triangles et fléchettes
Si g est le genre de X, N le degré du
dessin, a le nombre de zéros, b le nombre de uns
et c le nombre de faces,
la caractéristique d'Euler vaut :
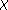 = 2 - 2g
= a + b + c - N
= 2 - 2g
= a + b + c - N
c. Groupes
Étant donnée une triangulation tripartite
sur une surface (non nécessairement orientée) X,
nous définissons une action sur les triangles :
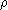 0,
0,
 1,
1,
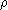
 associent respectivement à un triangle son symétrique
par rapport aux côtés
associent respectivement à un triangle son symétrique
par rapport aux côtés
 -
-
 ,
,
 -
-
 et
et
 -
-
 .
Ce sont les générateurs du groupe hypercartographique H2 = <
.
Ce sont les générateurs du groupe hypercartographique H2 = <
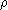 0,
0,
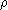 1,
1,
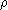
 |
|
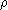 02 =
02 =
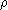 12 =
12 =
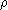
 2 = 1 >
(nous utilisons les notations de Jones et Singerman
[26]).
2 = 1 >
(nous utilisons les notations de Jones et Singerman
[26]).
Étant donné un dessin (sur une surface orientée X)
nous définissons aussi
une action sur les flèches :
en un sommet se rencontrent plusieurs
flèches, qu'on ordonne selon l'orientation
de la surface. Cette action associe à une
flèche la suivante autour du sommet
considéré.
Par définition,
 0,
0,
 1 et
1 et

 agissent respectivement par rotation autour des
agissent respectivement par rotation autour des
 ,
,
 ,
,
 .
Ils engendrent le groupe hypercartographique orienté
H2+ = <
.
Ils engendrent le groupe hypercartographique orienté
H2+ = <
 0,
0,
 1,
1,

 |
|
 0
0
 1
1

 = 1 >.
On peut remarquer que H2+ est le sous-groupe
d'indice 2 de H2 engendré par
= 1 >.
On peut remarquer que H2+ est le sous-groupe
d'indice 2 de H2 engendré par
 0 =
0 =
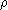 1
1
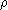
 ,
,
 1 =
1 =
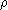

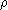 0
et
0
et

 =
=
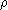 0
0
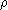 1
.
On peut aussi remarquer que H2+ est isomorphe au
groupe libre engendré
par
1
.
On peut aussi remarquer que H2+ est isomorphe au
groupe libre engendré
par  0
et
0
et  1.
1.
Présentation 5
(Sous-groupes d'indice fini)
Les dessins sont en correspondance avec
les classes de conjugaison de sous-groupes d'indice fini
du groupe hypercartographique H2+.
Le stabilisateur d'une flèche est un sous-groupe B
d'indice fini de H2+, l'action de ce groupe
sur B et ses translatés est identique à l'action sur
les flèches. Elle est identique pour tous les conjugués
de B.
En sens inverse, nous pouvons reconstruire un dessin
comme Schneps [37, p53] par recollement
des triangles d'une triangulation, ou bien comme
Jones et Singerman [26, p124]
par quotient d'une hypercarte universelle de type [p,q,r].
On dit qu'une hypercarte (un dessin) est de type [p,q,r]
si ces nombres (qui peuvent prendre la valeur
 )
sont des multiples des valences
des hyper-faces, hyper-arêtes et hyper-sommets.
Les groupes triangulaires orientés, ou fuchsiens,
agissent sur les flèches de tels dessins.
On note ces groupes
)
sont des multiples des valences
des hyper-faces, hyper-arêtes et hyper-sommets.
Les groupes triangulaires orientés, ou fuchsiens,
agissent sur les flèches de tels dessins.
On note ces groupes
 (p,q,r) = <
(p,q,r) = <
 0,
0,
 1,
1,

 |
|
 0p
=
0p
=
 1q
=
1q
=

 r
=
r
=
 0
0
 1
1

 = 1 > .
= 1 > .
Présentation 6
(Sous-groupes d'indice fini, bis)
Les dessins sont en correspondance avec
les classes de conjugaison de sous-groupes d'indice fini
d'un groupe triangulaire
 (p,q,r)
où p, q et r sont finis.
(p,q,r)
où p, q et r sont finis.
L'action de ce groupe sur les d flèches d'un dessin
se traduit par une représentation du groupe dans le
groupe de permutations
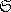 d.
d.
Présentation 7
(Triplets de permutations)
Un dessin est aussi un triplet de permutations
( 0,
0,
 1,
1,

 )
opérant transitivement sur un ensemble
fini (de flèches), telles que
)
opérant transitivement sur un ensemble
fini (de flèches), telles que
 0
0
 1
1

 = 1 ,
défini à conjugaison près
(renumérotation de l'ensemble des flèches).
= 1 ,
défini à conjugaison près
(renumérotation de l'ensemble des flèches).
Les sommets  (resp.
(resp.  ou
ou  )
sont en correspondance avec les cycles (orbites)
de
)
sont en correspondance avec les cycles (orbites)
de  0
(resp.
0
(resp.  1
ou
1
ou 
 ),
la valence du sommet est égale à la longueur
du cycle.
Cette présentation des hypercartes
comme triplet de permutations est
très classique et les hypercartes
sont parfois définies en tant que
permutations [15].
),
la valence du sommet est égale à la longueur
du cycle.
Cette présentation des hypercartes
comme triplet de permutations est
très classique et les hypercartes
sont parfois définies en tant que
permutations [15].
À cause de la présentation P8
d'un dessin comme revêtement ramifié,
nous appelons monodromie
le triplet
( 0,
0,
 1,
1,

 ),
qui correspond à l'action du
),
qui correspond à l'action du
 1
sur le revêtement.
La monodromie du dessin
de la figure II.5 est par exemple :
1
sur le revêtement.
La monodromie du dessin
de la figure II.5 est par exemple :

 =
(1,2,6,5,8,7,4),
=
(1,2,6,5,8,7,4),
 0 =
(1,4,5,6)(2,3),
0 =
(1,4,5,6)(2,3),
 1 =
(1,2,3)(5,7,8).
1 =
(1,2,3)(5,7,8).
II.2.2 Variantes
a. Marquage
Si l'une des faces (cellules  ) du dessin
est distinguée des autres,
il s'agit d'un dessin marqué.
Ceux-ci ont des propriétés algébriques
un peu plus simples qu'en l'absence
de marquage.
Ils interviennent lors de l'étude du
groupe modulaire
) du dessin
est distinguée des autres,
il s'agit d'un dessin marqué.
Ceux-ci ont des propriétés algébriques
un peu plus simples qu'en l'absence
de marquage.
Ils interviennent lors de l'étude du
groupe modulaire
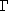 (1) =
PSL2(Z) et
de son sous-groupe de congruence
(1) =
PSL2(Z) et
de son sous-groupe de congruence
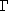 (2).
Birch les appelle drawings [7].
(2).
Birch les appelle drawings [7].
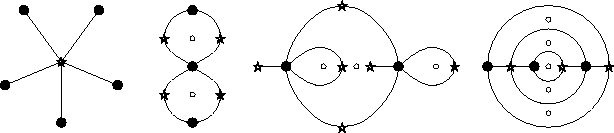
Figure II.7: Exemples de dessins marqués de genre 0
(dans le plan).
Si le dessin n'a qu'une face,
celle-ci est donc naturellement marquée.
En genre 0, le graphe correspondant
n'a pas de cycle.
On dit alors que le dessin est un arbre.
Les arbres ont une importance particulière parmi
les dessins d'enfants : leur étude est
plus facile et peut suffire, par exemple
lorsqu'on cherche à caractériser l'action
de Gal(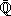 / Q)
sur les dessins.
/ Q)
sur les dessins.
b. Restrictions de valences
Si nous demandons à ce que les sommets  aient une valence égale à 2, nous pouvons
regrouper deux à deux les arêtes
et le dessin est alors une carte de X,
ayant pour sommets les
aient une valence égale à 2, nous pouvons
regrouper deux à deux les arêtes
et le dessin est alors une carte de X,
ayant pour sommets les
 et ayant une
et ayant une  sur chaque arête.
Lorsqu'on trace ces dessins, on omet habituellement
de placer les
sur chaque arête.
Lorsqu'on trace ces dessins, on omet habituellement
de placer les  au milieu des arêtes.
Nous les appelons les dessins propres
(clean, ou pure).
C'est ce que Shabat et Voevodsky ont
appelé dessin [43].
au milieu des arêtes.
Nous les appelons les dessins propres
(clean, ou pure).
C'est ce que Shabat et Voevodsky ont
appelé dessin [43].
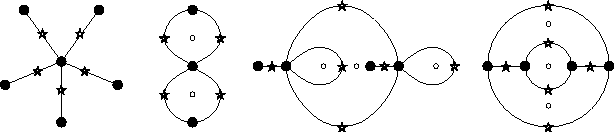
Figure II.8: Exemples de dessins propres.
Si nous acceptons des sommets  de
valence 1 ou 2, il s'agit d'un
dessin cartographique.
de
valence 1 ou 2, il s'agit d'un
dessin cartographique.
 Ils correspondent au groupe cartographique orienté C2+ =
Ils correspondent au groupe cartographique orienté C2+ =
 (
( ,2,
,2, ).
).
Ces deux variantes sont les plus étudiées
par les combinatoriciens.
Si les sommets  sont de valence 1 ou 3
et les sommets
sont de valence 1 ou 3
et les sommets  de valence 1 ou 2,
nous avons les dessins triangulaires.
Ils correspondent au groupe triangulaire orienté T2+ =
de valence 1 ou 2,
nous avons les dessins triangulaires.
Ils correspondent au groupe triangulaire orienté T2+ =
 (
( ,2,3).
,2,3).
Les dessins triangulaires marqués servent
par exemple à l'étude du
groupe modulaire PSL2(Z).
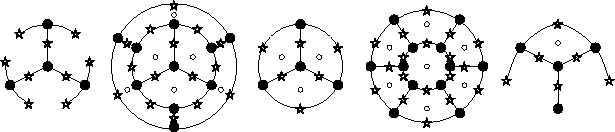
Figure II.9: Exemples de dessins triangulaires.
Si les sommets  sont tous de même valence p,
les sommets
sont tous de même valence p,
les sommets  de même valence q
et les cellules de même valence r,
nous avons les dessins semi-réguliers.
Les dessins galoisiens (c'est-à-dire les dessins
dont le nombre des automorphismes est égal
au degré, on les appelle aussi dessins réguliers)
sont des dessins semi-réguliers,
la réciproque est fausse en genre > 0.
de même valence q
et les cellules de même valence r,
nous avons les dessins semi-réguliers.
Les dessins galoisiens (c'est-à-dire les dessins
dont le nombre des automorphismes est égal
au degré, on les appelle aussi dessins réguliers)
sont des dessins semi-réguliers,
la réciproque est fausse en genre > 0.
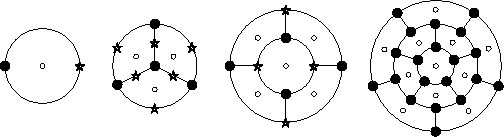
Figure II.10: Exemples de dessins (semi-)réguliers
de genre 0.
c. Dessin sur une surface quelconque
Nous avons défini les dessins sur une surface X,
compacte, connexe et orientable.
La surface X peut être munie d'une
structure de courbe algébrique
(variété algébrique de dimension 1)
ou de surface de Riemann (analytique
de dimension 1 sur C).
Si X est une surface connexe, éventuellement
non orientable, éventuellement avec un bord.
Il est encore possible d'y tracer un graphe
cellulaire (bipartite), mais cette surface
n'a pas la même richesse algébrique
et analytique.
L'étude de cette généralisation des dessins d'enfants
est faite par exemple par Jones et Singerman
[26].
Elle ne présente que peu d'intérêt pour nous
puisque ces dessins n'ont pas les propriétés
algébriques permettant d'étudier l'aspect arithmétique
d'un revêtement.
d. Sous-groupes du groupe modulaire
L'étude des sous-groupes du groupe modulaire
et de leur action sur le plan hyperbolique
est une façon de s'intéresser aux dessins
d'enfants
[2, 7].
On rappelle que le groupe modulaire
PSL2(Z) =
SL2(Z) / {±I} =
{±Mat(a,b;c,d)
| a, b, c et d éléments de Z
et ad-bc = 1}
agit sur le demi-plan hyperbolique sous
la présentation
PSL2(Z) =
{z 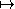 (az+b) / (cz+d)
| a, b, c et d éléments de Z
et ad-bc = 1}
(az+b) / (cz+d)
| a, b, c et d éléments de Z
et ad-bc = 1}
Parmi ses sous-groupes on distingue
les sous-groupes de congruence, par exemple
les 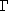 (n)
tels que b et c soient congrus à 0 modulo n.
(n)
tels que b et c soient congrus à 0 modulo n.
Le groupe triangulaire orienté T2+
peut être identifié au groupe
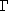 (1) =
PSL2(Z)
et le groupe hypercartographique orienté H2+
au sous-groupe de congruence
(1) =
PSL2(Z)
et le groupe hypercartographique orienté H2+
au sous-groupe de congruence
 (2),
mais il faut remarquer que l'injection canonique
du sous-groupe des translations
Z
(2),
mais il faut remarquer que l'injection canonique
du sous-groupe des translations
Z  PSL2(Z),
avec
n
PSL2(Z),
avec
n  (z
(z  z+n),
définit un marquage du dessin correspondant.
C'est pour cela que lorsqu'on aborde ainsi les
dessins d'enfants,
on considère les dessins marqués
z+n),
définit un marquage du dessin correspondant.
C'est pour cela que lorsqu'on aborde ainsi les
dessins d'enfants,
on considère les dessins marqués
II.2.3 Aspect géométrique
Nous avons donc défini les dessins d'enfants
topologiquement comme un graphe
à l'intérieur d'une surface X, sans en fixer
la position dans cette surface.
Il existe une définition équivalente,
comme revêtement de P1 moins trois points,
qui donne la ``vraie'' forme d'un dessin
en imposant la forme de ce graphe.
a. Revêtement complexe ramifié
Présentation 8
(Revêtement)
On s'intéresse aux revêtements finis
 :
X
:
X P1C
ramifiés au dessus de
0, 1,
P1C
ramifiés au dessus de
0, 1,  seulement,
à
seulement,
à  -isomorphisme près.
-isomorphisme près.
Cette définition d'un dessin d'enfant est équivalente aux
définitions topologiques.
Ceci est la Correspondance de Grothendieck.
On fait se correspondre la monodromie
du revêtement et la présentation du dessin comme
triplet de permutations.
Un dessin d'enfant, au sens de
P5,
est en bijection avec les classes de
conjugaison des sous-groupes d'indice fini de H2+.
Or  1,
le groupe fondamental de P1C - {0, 1,
1,
le groupe fondamental de P1C - {0, 1,  },
engendré par les trois boucles autour
de 0, 1 et
},
engendré par les trois boucles autour
de 0, 1 et  , est isomorphe au
groupe H2+.
, est isomorphe au
groupe H2+.
Un théorème classique (par exemple
[37, lemme I.1, p48])
prouve que les classes de conjugaison des sous-groupes d'indice fini
de  1
sont en bijection avec les revêtements finis
de P1C - {0, 1,
1
sont en bijection avec les revêtements finis
de P1C - {0, 1,  }.
Si B est un sous-groupe d'indice fini
de
}.
Si B est un sous-groupe d'indice fini
de  1 et
si X est le revêtement universel de P1C -
{0, 1,
1 et
si X est le revêtement universel de P1C -
{0, 1,  },
alors le quotient B \ X définit un revêtement fini,
et réciproquement B est le stabilisateur
dans
},
alors le quotient B \ X définit un revêtement fini,
et réciproquement B est le stabilisateur
dans  1
d'un point du revêtement.
1
d'un point du revêtement.
b. Correspondance de Grothendieck d'un point de vue élémentaire
Visuellement, cette correspondance s'obtient comme suit :
à partir d'un revêtement
 :
X
:
X P1C,
la préimage sur X du segment [0, 1]
inclus dans P1C trace un dessin.
L'ensemble fini
P1C,
la préimage sur X du segment [0, 1]
inclus dans P1C trace un dessin.
L'ensemble fini
 -1(0)
est l'ensemble des
sommets
-1(0)
est l'ensemble des
sommets  ,
l'ensemble
,
l'ensemble
 -1(1)
contient les
-1(1)
contient les  , et
, et
 -1(
-1( )
les
)
les  .
Les flèches sont les composantes de
.
Les flèches sont les composantes de  -1(]0, 1[),
qui relient les
-1(]0, 1[),
qui relient les  et les
et les  .
De même,
.
De même,
 -1(]1,
-1(]1,
 [)
relie les
[)
relie les  et
et
 et
et  -1(]
-1(] , 0[)
relie les
, 0[)
relie les  et
et  .
Nous avons ainsi une triangulation
(P2 et
P3)
et les triangles de chaque type sont les préimages de
chaque demi-sphère P1C - R.
.
Nous avons ainsi une triangulation
(P2 et
P3)
et les triangles de chaque type sont les préimages de
chaque demi-sphère P1C - R.
Dans l'autre sens, on part d'une triangulation bicolorée
et on construit l'application
 en envoyant chaque triangle dans la demi-sphère
P1C - R correspondant
au type du triangle.
On utilise par exemple le théorème d'existence
de Riemann pour relever une structure complexe.
en envoyant chaque triangle dans la demi-sphère
P1C - R correspondant
au type du triangle.
On utilise par exemple le théorème d'existence
de Riemann pour relever une structure complexe.
L'application  est appelée application de Belyi.
Toute fonction rationnelle sur X ayant au plus trois
valeurs critiques est une application de Belyi.
En effet, le choix du triplet
{0, 1,
est appelée application de Belyi.
Toute fonction rationnelle sur X ayant au plus trois
valeurs critiques est une application de Belyi.
En effet, le choix du triplet
{0, 1,  } n'est pas
limitatif puisque tout triplet de points rationnels de P1
peut être envoyé par une homographie sur
{0, 1,
} n'est pas
limitatif puisque tout triplet de points rationnels de P1
peut être envoyé par une homographie sur
{0, 1,  }.
Parfois, on choisit {0, 1728,
}.
Parfois, on choisit {0, 1728,
 }, lorsqu'on
étudie le groupe modulaire [2,
7].
}, lorsqu'on
étudie le groupe modulaire [2,
7].
c. Aspect arithmétique
La contribution de Belyi [5]
est la suivante. On peut
tracer un dessin d'enfant sur n'importe quelle courbe
définie sur  .
.
Théorème 1
(Belyi)
Soit X une courbe algébrique (projective, connexe et lisse)
définie sur C.
Alors X est une courbe arithmétique si et seulement s'il existe
un revêtement ramifié
 :
X
:
X P1C,
tel que ses valeurs critiques soient dans
{0, 1,
P1C,
tel que ses valeurs critiques soient dans
{0, 1,  }.
Le couple (X,
}.
Le couple (X,
 )
est appelé paire de Belyi.
)
est appelé paire de Belyi.
- Preuve
-
Le sens si est une conséquence
(pas si évidente [47])
d'un critère de Weil.
La preuve de l'autre sens, due à Belyi, se fait en construisant
 à partir d'une fonction
à partir d'une fonction 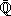 -rationnelle quelconque sur X.
-rationnelle quelconque sur X.
On procède en deux étapes : on diminue le nombre
de valeurs critiques non rationnelles, au prix
d'une augmentation de la ramification au dessus
de l'infini, puis on diminue le nombre de valeurs
critiques finies, jusqu'à ce qu'il n'en reste
que deux.
Une courbe arithmétique est par définition
une courbe algébrique définie sur
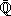 .
Un élément
.
Un élément
 de son corps des fonctions sur
de son corps des fonctions sur
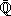 définit un revêtement de P1
ramifié sur un sous-ensemble fini de P1(
définit un revêtement de P1
ramifié sur un sous-ensemble fini de P1(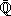 ).
).
La première étape se fait en composant à gauche
 par une suite de polynômes diminuant le
nombre de valeurs critiques non rationnelles.
Soit C l'ensemble des valeurs critiques de
par une suite de polynômes diminuant le
nombre de valeurs critiques non rationnelles.
Soit C l'ensemble des valeurs critiques de
 non rationnelles et leurs conjuguées par Gal(
non rationnelles et leurs conjuguées par Gal(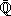 / Q).
Soit h le polynôme à coefficients
rationnels s'annulant sur C.
Alors les valeurs critiques de h o
/ Q).
Soit h le polynôme à coefficients
rationnels s'annulant sur C.
Alors les valeurs critiques de h o
 sont 0,
sont 0,  et les valeurs critiques de h,
qui seront annulées par un polynôme de degré
strictement inférieur à d°h.
et les valeurs critiques de h,
qui seront annulées par un polynôme de degré
strictement inférieur à d°h.
La seconde étape se fait en composant à gauche
par des polynômes de la forme ci-dessous, qui
envoient les valeurs critiques
{ ,
0, 1, m/(m+n)} en
{
,
0, 1, m/(m+n)} en
{ , 0, 1},
et réduisent donc le nombre de valeurs critiques rationnelles.
, 0, 1},
et réduisent donc le nombre de valeurs critiques rationnelles.
z 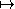 (m+n)m+n/(mmnn)
zm(1-z)n
(m+n)m+n/(mmnn)
zm(1-z)n
Belyi a proposé une variante de cette seconde
étape, où on compose par une unique fraction
rationnelle, dont les points de ramification
sont des entiers positifs, et dont les valeurs
de ramification sont {0, 1,  }.
De telles fractions rationnelles sont les fonctions
de Belyi d'une famille de dessins d'enfants,
pour lesquels il a donné une construction
explicite (cf. § III.2.1.b.).
}.
De telles fractions rationnelles sont les fonctions
de Belyi d'une famille de dessins d'enfants,
pour lesquels il a donné une construction
explicite (cf. § III.2.1.b.).
II.2.4 Généralisations
a. Revêtements de la sphère
Nous pouvons considérer les revêtements
 :
X
:
X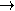 P1
ramifiés au dessus de k>3 points.
Comme Adrianov et Shabat [1],
nous pouvons appeler
P1
ramifiés au dessus de k>3 points.
Comme Adrianov et Shabat [1],
nous pouvons appeler
 une
fonction de Fried si k=4, mais ce terme n'a
pas la même audience que ``fonction de Belyi''.
Contrairement au cas des fonctions de Belyi,
la position relative dans P1 des 4 valeurs
de ramification change les propriétés
algébriques du dessin.
une
fonction de Fried si k=4, mais ce terme n'a
pas la même audience que ``fonction de Belyi''.
Contrairement au cas des fonctions de Belyi,
la position relative dans P1 des 4 valeurs
de ramification change les propriétés
algébriques du dessin.
b. Graphes enrubannés
Partant d'une paire de Belyi (X,  ),
nous traçons sur X la préimage du cercle
unité.
Nous obtenons ainsi une carte sur X
ayant un
),
nous traçons sur X la préimage du cercle
unité.
Nous obtenons ainsi une carte sur X
ayant un  ou un
ou un  au centre
de chaque face (les faces sont donc de deux couleurs)
et dont les sommets
sont des
au centre
de chaque face (les faces sont donc de deux couleurs)
et dont les sommets
sont des  et sont de valence paire.
et sont de valence paire.
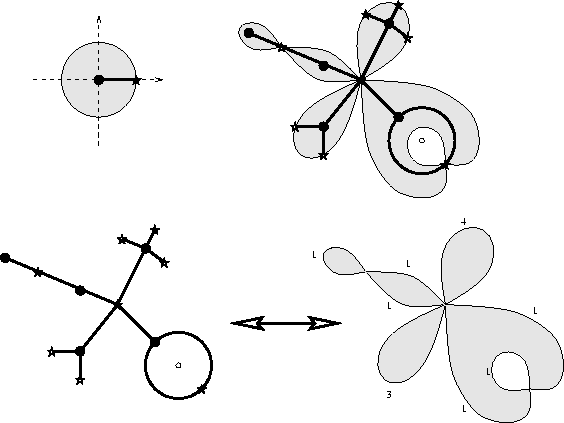
Figure II.11: Dessins et graphes enrubannés.
Selon la terminologie de [49],
un graphe enrubanné est une
carte dont tous les sommets ont
pour valence au moins 3.
Un graphe enrubanné est orientable
s'il est possible de le munir d'une
bicoloration des cellules.
Les valences des sommets sont alors
toutes paires.
Si on ignore les  de valence 2,
la préimage du cercle unité est
donc un graphe enrubanné orienté.
de valence 2,
la préimage du cercle unité est
donc un graphe enrubanné orienté.
Pour avoir une bijection,
nous devons associer à chaque arête
du graphe enrubanné un entier positif,
sa longueur, qui est est égale au
nombre de  sur l'arête, plus un.
sur l'arête, plus un.
Les graphes enrubannés métriques
sont les graphes enrubannés dont
chaque arête est étiquetée par
un réel positif, sa longueur.
Ils forment donc une généralisation
(topologique) des dessins d'enfants.
c. Différentielles de Strebel
Les différentielles de Strebel
sont aux graphes enrubannés métriques
ce que les applications de Belyi
sont aux dessins d'enfants.
Une forme différentielle quadratique
 n'ayant que des pôles doubles est
une différentielle de Strebel si on peut y associer
n'ayant que des pôles doubles est
une différentielle de Strebel si on peut y associer
 un graphe critique
un graphe critique
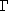 qui délimite une
décomposition cellulaire de la surface X.
qui délimite une
décomposition cellulaire de la surface X.
Un théorème de Strebel [44]
montre que pour tout n-uplet
de points distincts P1, ..., Pn étiquetés par des
réels strictement positifs p1, ..., pn,
il existe une et une seule différentielle
de Strebel ayant P1, ..., Pn comme pôles
et p1, ..., pn comme périmètre des faces
correspondantes.
Si (X,  ) est une paire de Belyi,
nous voyons X comme une surface de Riemann
et
) est une paire de Belyi,
nous voyons X comme une surface de Riemann
et  comme une fonction méromorphe
sur X.
Nous pouvons construire
la forme différentielle méromorphe
comme une fonction méromorphe
sur X.
Nous pouvons construire
la forme différentielle méromorphe
 =
d
=
d /
(2
/
(2 i
i ).
Son carré
).
Son carré

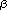 =
(
=
(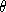
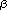 )
) 2
est une différentielle de Strebel dont le graphe
critique est aussi le graphe enrubanné préimage
du cercle unité par
2
est une différentielle de Strebel dont le graphe
critique est aussi le graphe enrubanné préimage
du cercle unité par  .
.
Le problème de la rationalité ou de l'algébraïcité
des paramètres d'une différentielle de Strebel
n'est pas facile.
![]() {
{![]() ,
,
![]() }
donnant un type aux sommets, telle que chaque arête
soit adjacente à deux sommets de types
différents.
}
donnant un type aux sommets, telle que chaque arête
soit adjacente à deux sommets de types
différents.






