IV.3 Les arbres en Y
IV.3.1 Classification
a. Énumération
On étudie la famille
des arbres ayant un unique sommet de valence 3,
tous les autres étant de valence 1 ou 2.
Si les branches de l'arbre ont pour longueurs a,b,c,
Pakovitch [36, chap. 2] les note
Ya,b,c.
Nous les appelons arbres en Y ou Y-arbres.
Comme pour tous les arbres, nous séparons les
sommets des arbres en Y en deux types
 et
et
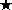 .
Les types des trois sommets de valence 1
forment un invariant Galoisien qui détermine
quatre familles d'arbres en Y.
Nous supposons que le sommet de valence 3 est de type
.
Les types des trois sommets de valence 1
forment un invariant Galoisien qui détermine
quatre familles d'arbres en Y.
Nous supposons que le sommet de valence 3 est de type
 et nous comptons le nombres d'arbres de chaque type
avec la formule du paragraphe II.3.4.
Ici, k est un entier naturel quelconque.
et nous comptons le nombres d'arbres de chaque type
avec la formule du paragraphe II.3.4.
Ici, k est un entier naturel quelconque.
- [Type A] Extrémités de types
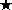 ,
,
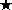 ,
,
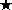 .
.
Il y a nA(k) = (k+1)(k+2) / 6
dessins de type [3+2k; 3 2k; 2k 13].
- [Type B] Extrémités de types
 ,
,
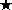 ,
,
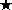 .
.
Il y a nB(k) = (k+1)(k+2) / 2
dessins de type [4+2k; 3 2k 1; 2k+1 12].
- [Type C] Extrémités de types
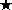 ,
,
 ,
,
 .
.
Il y a nC(k) = (k+1)(k+2) / 2
dessins de type [5+2k; 3 2k 12; 2k+2 1].
- [Type D] Extrémités de types
 ,
,
 ,
,
 .
.
Il y a nD(k) = (k+1)(k+2) / 6
dessins de type [6+2k; 3 2k 13; 2k+3].
On remarque que si k est un multiple de 3,
les nombres nA(k) et
nD(k) ne sont pas entiers.
La valeur 1/3 correspond à l'arbre dont les trois branches
sont de longueurs égales ((2k+6)/3 ou (2k+3)/3),
qui admet un automorphisme d'ordre 3
(la rotation d'un tiers de tour).
b. Action de Galois
Voici ce qu'on peut conjecturer sur les orbites
sous l'action de Galois.
La preuve de la dernière conjecture est immédiate,
car les branches des Y-arbres de type D sont de longueur
paire.
Ces conjectures font que les Y-arbres de type B ou C
sont de bons candidats pour avoir des corps des modules
 de degré assez élevé, ce qui permet de tester nos algorithmes.
de degré assez élevé, ce qui permet de tester nos algorithmes.
-
Les Y-arbres de type A sont les conjugués des Y1,1,2k+1
et les multiples impairs de ces arbres
(cette conjecture est vérifiée pour k < 13).
-
Les Y-arbres de type B sont les conjugués des Y1,1,2k+2
et les multiples impairs de ces arbres
(cette conjecture est vérifiée pour k < 11).
-
Les Y-arbres de type C sont les conjugués des Y2,2,2k+1
et les multiples impairs de ces arbres
(cette conjecture est vérifiée pour k < 10).
-
Les Y-arbres de type D sont les doubles
(au sens du § II.3.3.c.)
d'un autre Y-arbre de degré moitié.
Nous appelons donc Y-arbre irréductible
un arbre Y1,1,N-2 ou un arbre Y2,2,2k+1.
Nous vérifions notre conjecture en calculant
le degré des corps des modules des Y-arbres
irréductibles.
IV.3.2 Résultats
a. Description des tables
La première table donne, pour les Y-arbres de
type B, les temps et mémoire utilisés pour
le calcul d'un polynôme P
définissant le corps des modules.
On voit que la méthode numérique est au moins
aussi performante qu'une utilisation classique
de bases de Gröbner.
Une seconde table donne, pour les Y-arbres de
type A, B ou C la longueur des orbites galoisiennes.
On donne le discriminant du corps des modules
des Y-arbres irréductibles, ou un multiple de
ce discriminant si le calcul est impraticable.
La troisième table donne les polynômes P
obtenus par nos calculs.
Lorsque le corps est de petit degré, nous
donnons aussi un autre polynôme Q, unitaire,
définissant le corps des modules
de façon un peu plus canonique
(voir l'algorithme polred
[11, p166]).
Voici quelques précisions sur le calcul du polynôme P :
pour les arbres de type B, on place le sommet  de valence 3 en 0, le sommet
de valence 3 en 0, le sommet  de valence 1 en 1,
et le polynôme P est le polynôme minimal de la
somme des deux sommets
de valence 1 en 1,
et le polynôme P est le polynôme minimal de la
somme des deux sommets 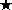 de valence 1.
de valence 1.
Pour les arbres de type C, on place le sommet  de valence 3 en 0, le sommet
de valence 3 en 0, le sommet 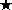 de valence 1 en 1,
et le polynôme P est le polynôme minimal de la
somme des deux sommets
de valence 1 en 1,
et le polynôme P est le polynôme minimal de la
somme des deux sommets  de valence 1.
de valence 1.
Pour les arbres de type A, si nous plaçons
le sommet de valence 3 en 0
et si nous imposons la somme des sommets
de valence 1 à 1,
alors la somme des sommets de même type est
toujours rationnelle.
Le polynôme P est donc ici le polynôme minimal
de la deuxième fonction symétrique
des trois sommets de valence 1.
Le calcul de d(K) est bien plus lent
et ne peut être mené à terme que pour les petits corps de
définition.
Pour B(5), le calcul de d(K) à l'aide de Pari
(algorithme Round 4)
met 120 heures en utilisant 450 Mo de mémoire.
Il faut construire une base intégrale
de K, à partir d'un ordre que l'on grossit pour chaque nombre
premier.
Les algorithmes Round 4 et Round 2 implantés dans Pari
partent de l'ordre engendré par une racine d'un polynôme P unitaire.
Comme le coefficient dominant des polynômes que nous calculons
a de nombreux petits facteurs, ces algorithmes perdent beaucoup
de temps à éliminer ces facteurs.
Il serait donc utile de développer une extension de ces algorithmes
aux ordres engendrés par un P quelconque.
b. Le choix de l'approximation initiale
Pour le calcul par approximation
se pose le problème du choix de
la position initiale des sommets
de l'arbre.
Sa solution est ici très facile.
Une première approche est de calculer
les propriétés de Y1,1,n en
calculant successivement Y1,1,1 ,
Y1,1,2 , ..., Y1,1,n-1
et Y1,1,n ,
chacun s'obtenant par rajout d'un point
dans la branche la plus longue du précédent.
Nos considérations sur l'aspect du tracé
d'un dessin dans le plan suggèrent que
la longueur de cette branche a peu
d'influence sur ce qui se passe à ses
extrémités.
Nous choisissons donc de remplacer
l'arête du milieu (qui est aussi
la plus longue) par deux arêtes
ayant cette longueur.
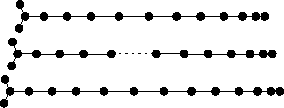
Une seconde approche est de remarquer
que l'arbre Y1,1,n est "similaire"
à la ligne avec n+2 sommets,
dont on connaît bien la fonction de Belyi
(polynôme de Tchebitchev).
Puisque nous savons qu'au voisinage d'un sommet de
valence 3, les arêtes font un angle 1/3 de tour,
nous remplaçons la dernière arête de la ligne par
deux arêtes de même longueur, symétriques.
Chacune de ces deux approches permet d'être
dans la zone de convergence de l'algorithme
de Newton.

c. Performance des différentes méthodes
| sur SS20/71
| B(5) | B(6) | B(7) | B(8) | B(9) | B(10)
|
| Maple : mini
|
|
|
|
|
|
|
| Maple : standard
|
|
|
|
|
|
|
| MuPAD
|
|
|
|
|
|
|
| | modular
| | | comput.
| | GB | check
| | | totolex
| | | mémoire
|
|
|
| 0.5s
| | 0.6s
| | 2.3s
| | 213s
| | 13 Mo
|
|
| 0.8s
| | 2.3s
| | 6.5s
| | 19 min
| | 23 Mo
|
|
| 1.9s
| | 5.8s
| | 17s
| | 94 min
| | 46 Mo
|
|
| 4.6s
| | 14s
| | 47s
| | 613 min
| | 109 Mo
|
|
|
| Numérique
| | convergence
| | LLL
| | précision
| | mémoire
|
|
|
|
|
| |
| 44 min
| | 9 min
| | 1900 d
| | 30 Mo
|
|
| |
| 108 min
| | 35 min
| | 3200 d
| | 52 Mo
|
|
| |
| 242 min
| | 114 min
| | 3900 d
| | 56 Mo
|
|
d. Discriminant du corps de définition
- nA(0) = 1/3.
Q.
- nA(1) = 1.
Q.
- nA(2) = 2.
d(K) = 3 7.
- nA(3) = 3 + 1/3.
d(K) = -33 5.
L'orbite de longueur 1 est le triple de A(0) .
- nA(4) = 5.
d(K) = -33 52 7 113.
- nA(5) = 7.
d(K) = 34 53 72
136.
- nA(6) = 8 + 1 + 1/3.
d(K) = -37 57 73 11.
Les orbites de longueur 1 sont le quintuple de A(0)
et le triple de A(1).
- nA(7) = 12.
d(K) = 38 55 74
112 13 1710.
- nA(8) = 15.
d(K) = -312 57 75
113 132 1913.
- nA(9) = 16 + 2 + 1/3.
d(K) = -314 57 715
114 133 17.
L'orbite de longueur 1 est le septuple de A(0)
et celle de longueur 2 le triple de A(2).
- nA(10) = 22.
d(K) = 318 511 77
115 134 172 19 2319.
- nA(11) = 25 + 1.
d(K) = 317 543 79
116 135 173 192.
L'orbite de longueur 1 est le quintuple de A(1)
- nA(12) = 27 + 3 + 1/3.
d(K) = -365 512 79
117 136 174 193 23.
L'orbite de longueur 1 est le nonuple de A(0)
et celle de longueur 3 le triple de A(3).
- nC(0) = 1.
Q.
- nC(1) = 3.
d(K) = -22 3 72
- nC(2) = 6.
d(K) = 24 310 5.
- nC(3) = 10.
d(K) = 28 37 52 7
118
- nC(4) = 15.
d(K) = 212 310 55
72 1312
- nC(5) = 20 + 1.
d(K) = -216 319 520
73 11.
L'orbite de longueur 1 est le triple de C(0).
- nC(6) = 28.
d(K) = 224 322 511
76 112 13 1724.
- nC(7) = 36.
d(K)f2 = 23364 3592
5197 7121 1145 1332
19140 N2.
- nC(8) = 42 + 3.
d(K)f2 = -24560 381
5255 742 1164 1351
1719 N2.
L'orbite de longueur 3 est le triple de C(1).
- nC(9) = 55.
d(K)f2 = -27884
31352 5461 7233 1185
1372 1740 1921 23270
N2.
e. Polynômes caractérisant les corps de définition
- A(3)
- Q = x3 + 3x - 1,
P = 3x3 + 12x2 + 27x + 5.
- A(4)
- Q = x5 - x4 - 9x3
+ 3x2 - 9,
P = 361x5 - 4474x4 - 38273x3
- 65627x2 - 41455x - 4325.
- A(5)
- Q = x7 - 2x6 - 15x5
- 17x4 + 406x3 - 1185x2 + 1528x - 797,
P = 54289x7 - 282278x6 - 3283899x5
- 31969477x4 - 78654736x3 - 65823135x2
- 20988650x - 1404125.
- A(6)
- Q = x8 - x7 - 8x6 + 47x5
- 65x4 - 7x3 + 217x2 - 154x + 91,
P = 289x8 - 4885x7 - 46400x6
- 342915x5 - 1089480x4 - 1739622x3
- 996660x2 - 214785x - 10305.
- A(7)
- P = 98207651161x12 + 870318338439x11
- 225964214871x10 - 120603046889300x9
- 1641468242003715x8 - 8545487217454683x7
- 23874722290036452x6 - 38144830567619007x5
- 35366172814693935x4 - 18277692100532150x3
- 4874726982487875x2 - 585383786486250x - 19309256928125.
- A(8)
- P = 870144924171961x15 - 31272534505579827x14
+ 3409826827410834x13 + 1631528313606604292x12
+ 25545284053437227001x11 + 265781178080254774527x10
+ 1656478912849790418811x9 + 6206289995712665940813x8
+ 14144169927465834515019x7
+ 20094178519992806367157x6
+ 17902864566095038971675x5
+ 9866732665267344460200x4
+ 3223408046591823300500x3 + 576457341066342065625x2
+ 48553143846669318750x + 1206449284005015625.
- A(9)
- P = 92811821263x16 + 2185900990315x15
+ 45151781389620x14 + 529427232145945x13
+ 4647506123797600x12 + 28962371220779367x11
+ 128594938811688720x10 + 406119437724414015x9
+ 902761895287107765x8 + 1392468619368942000x7
+ 1462963566390250932x6 + 1022154080759090055x5
+ 457850422093506750x4 + 123967037149475625x3
+ 18361060568707500x2 + 1270568722106250x + 25781283703125.
- A(10)
- P = 51109675742232059162815081x22
- 1222855031957479455016606244x21
- 33339533013059925808858928358x20
- 176587156452636149850433811942x19
+ 348622602175388288979081326095x18
+ 24884847684057802873707363914604x17
+ 439207448836219867986760498269369x16
+ 4852935494438817287737345818051768x15
+ 35084749352147350986571673594602077x14
+ 173915157982809729913031460240111950x13
+ 609804567556133082118145018126777759x12
+ 1544739507078353087800675396870208289x11
+ 2860271423122088700985131214538825543x10
+ 3886404275079347133591396941957087822x9
+ 3865938157918915333099831680499340370x8
+ 2792815798059667267473122722875005625x7
+ 1444839482062782541267491192975673500x6
+ 523731890421570789353429311796881875x5
+ 128660108139561133850161428552428125x4
+ 20333324629864201224102987769890625x3
+ 1897902407627305324013017906406250x2
+ 89172188853981460591162052734375x
+ 1366808126272895577235041015625.
- A(11)
- P = 22028597127867789918064321x25
- 157097838122150956691122685x24
+ 1916846593202473307608849635x23
- 139509067092638121891060343885x22
- 1151394592136979970414782132790x21
+ 878364548094972935771145209370x20
+ 120462860834784888254767546254085x19
+ 2233088278804411372483919546447215x18
+ 25668425441333273660814531432522285x17
+ 205906551849460957881253465328405765x16
+ 1197031385121657648321833046341492720x15
+ 5120647423725156888101898981582221865x14
+ 16248704064188296821227381901541038460x13
+ 38471846683417178603653622531252181790x12
+ 68218639604342600499888216881238965535x11
+ 90689988351840735527561195514821924900x10
+ 90179757628905495914028778111875967610x9
+ 66667952668687129479428454167573728815x8
+ 36265830918014862670238503260679873060x7
+ 14292502185461894708632449353282818240x6
+ 3989224511813535581408140215071936265x5
+ 762493000918268063921002668712038140x4
+ 94772184968545561476484255568169185x3
+ 7037425341291554045535134429285565x2
+ 266306914994407378687794743366260x
+ 3360856796510637621867259412161.
- A(12)
- P = 62988609009298392434369403x27
- 2332551347079881215471219764x26
- 30668233624242162370408947285x25
- 529876740736746814114788761835x24
- 3877197676066819870808386257090x23
- 12660604020408321548374495522572x22
+ 369828433241452431712870952963526x21
+ 8546705458594281500723513941952610x20
+ 118186809580809328874131082522847735x19
+ 1132945527793722216977233510798248540x18
+ 7863182561861811687130578415618699176x17
+ 40601544033588737696927149755551661522x16
+ 157579908245340055362410583271625726085x15
+ 462292650354789103158368106241062332160x14
+ 1031209227170942595420802076785157258565x13
+ 1759046530728901161977714677041466452864x12
+ 2304051022208495839331341462080867395328x11
+ 2320576437670917405945143206327212499200x10
+ 1793453331972140397279079374458782875825x9
+ 1057037086516691965551691776388240026375x8
+ 469860326566059597781780345154823450000x7
+ 154808338577620452555653131847884987500x6
+ 36845230536646283953174746000283453125x5
+ 6098176957769173885488336550129218750x4
+ 662547205405272240602748452035546875x3
+ 43091047723513831384746029273437500x2
+ 1422986981521391200555139707031250x
+ 15522928406114874760081689453125.
- B(1)
- Q = x3 + 2,
P = 25x3 - 42x2 + 12x + 8.
- B(2)
- Q = x6 -2x5 -x4 +6x3
-2x2 -4x -1,
P = 192x6 + 1600x5 + 5488x4
+ 8464x3 + 5960x2 + 1784x + 137.
- B(3)
- Q = x10 - 5x9 - 10x8
- 330x7 + 3780x6 - 23538x5
+ 146520x4 - 900210x3 + 4617195x2
- 8099745x - 6066414,
P = 288x10 + 4920x9 + 37400x8
+ 154160x7 + 379100x6 + 574424x5
+ 534980x4 + 295250x3 + 89690x2
+ 12950x + 563.
- B(4)
- P = 5120x14 + 149504x13
+ 2014208x12 + 15777280x11 + 79923712x10
+ 275166208x9 + 658361216x8
+ 1101880256x7 + 1283578112x6
+ 1023671040x5 + 541541472x4
+ 180018720x3 + 34297616x2 + 3188528x + 92633.
- B(5)
- P = 24883200x21 + 1158312960x20
+ 25502867712x19 + 341618429376x18
+ 3109936201344x17 + 20392715344064x16
+ 99638796203968x15 + 370504764844224x14
+ 1062741483903680x13 + 2370640833511888x12
+ 4128644196255936x11 + 5614827771514976x10
+ 5942714032340512x9 + 4860315116093808x8
+ 3036961695710128x7 + 1425822458726372x6
+ 491072052205560x5 + 119836481716252x4
+ 19663328827436x3 + 1993132055040x2
+ 106550236828x + 2000024111.
- B(6)
- P = 513684799488000x28
- 34901212948070400x27
+ 1137545530142883840x26
- 23094430990658961408x25
+ 326698815564602671104x24
- 3421329382195643547648x23
+ 27523540095132109897728x22
- 174305408754660243668992x21
+ 883931948169484761563136x20
- 3633243437315754018471936x19
+ 12208911396657704553414656x18
- 33740348646985795280830464x17
+ 76979469564829984977911808x16
- 145292021332525428824211456x15
+ 226960358645737432122753024x14
- 293120952934211895334699008x13
+ 312191481069764390293626880x12
- 273058909744499620720631808x11
+ 194957884663016060566106112x10
- 112699121083547276423794688x9
+ 52176655480973862044680704x8
- 19071337921265203163214336x7
+ 5399626220939144567968512x6
- 1154053132723323568606464x5
+ 179599504361044758896448x4
- 19299434128448598021184x3
+ 1315528871847908959392x2
- 48630693359656374240x
+ 658418172827465249.
- B(7)
- P = 128450560000x33
- 11707809792000x32
+ 515906676326400x31
- 14320455719649280x30
+ 280278666945232896x29
- 4112010196865513472x28
+ 46962642048178507264x27
- 428236816106298382848x26
+ 3174061201133603157504x25
- 19372769702192537887488x24
+ 98305223546172769210368x23
- 417686500832906293682688x22
+ 1493724878756594616210432x21
- 4512769265396529128088576x20
+ 11546134536650775044859648x19
- 25052844127927284357151488x18
+ 46120547173023714432494592x17
- 72002596612591111053052800x16
+ 95199167018173601085387456x15
- 106357485558642750786858048x14
+ 100078973730597608483119488x13
- 78970049026910168467295136x12
+ 51958955637812070724883328x11
- 28299178126805457249292896x10
+ 12640465685125959112475328x9
- 4575645926936732962787328x8
+ 1321740712875893316349680x7
- 298567190658186756100976x6
+ 51320083437219286364736x5
- 6461987207673914870592x4
+ 563746426651493261606x3
- 31198295910054895890x2
+ 932905167417746466x
- 10118390704879427.
- B(8)
- P = 9394859377925554176x44
- 1173388111352495603712x43
+ 71448077328882874712064x42
- 2780015926599994476331008x41
+ 77422331852032749198114816x40
- 1642402295245685222446989312x39
+ 27595316583078351282125144064x38
- 377133789254279866596194254848x37
+ 4273710531384938117910522494976x36
- 40740319074997723094066053251072x35
+ 330353567266620648162945725890560x34
- 2298598756136751047199964822241280x33
+ 13819827277318218281101778464276480x32
- 72199011711251117446930106668810240x31
+ 329240635765647781433612734006558720x30
- 1315316548836346248737638889881075712x29
+ 4616808635541020223278013269566029824x28
- 14270281831217176293899375198515232768x27
+ 38908477686379152579596273809795055616x26
- 93691608427885137130668400469949284352x25
+ 199399791480130310728340908243358318592x24
- 375188476955331131897350251091432833024x23
+ 624058395359951497629690764814490533888x22
- 917109081104150047114685270652231745536x21
+ 1189659067560680152083638002026897211392x20
- 1360271723542821496081641704468433862656x19
+ 1368438842133738805764353493062580436992x18
- 1208369177810057324216201580820720779264x17
+ 933872161056270213473375312536066326528x16
- 629447879472638774118609414237634584576x15
+ 368452569953959818137395218403091770368x14
- 186363919646205211005540323730318759936x13
+ 80963231005465055431231309139582948352x12
- 29994223389861610018683069707826276864x11
+ 9394226540023502908676634116224409088x10
- 2461583279680711471859846831616316416x9
+ 532752680782978676549575414759642752x8
- 93722753670264864804888618414375744x7
+ 13131402670602394299584333377291008x6
- 1426531501133005458306557969858816x5
+ 115830768852467777831456275003424x4
- 6665669357160822264930339318368x3
+ 249931301580110806288721893936x2
- 5235606039815235509102372752x
+ 42053103397718025129673369.
- B(9)
- P = 6658606584104736522240000000x55
- 1078062755921157383258112000000x54
+ 85536161235193746456104140800000x53
- 4372046023231479792951676108800000x52
+ 161318471713543361535156840038400000x51
- 4574520993146953054496685405555916800x50
+ 103707882294023875517628438374976061440x49
- 1931270934412677931854105984358517047296x48
+ 30129018192497362894261512430781304668160x47
- 399670712380551271105623667681694981947392x46
+ 4560740470619315055913315131125369508888576x45
- 45186044503113285714192401156700103272726528x44
+ 391628020872984325108359303360288188439724032x43
- 2987662255558756424138422163024222389686190080x42
+ 20165726889847790015503205665809424787591135232x41
- 120947147363230360113039448128689659923564904448x40
+ 646928096224170808375771433166927677996422144000x39
- 3095483204201644325319387295590586420658051506176x38
+ 13284289524754136012455432333636432103560599347200x37
- 51242717333303827951863941148383589873061023444992x36
+ 177991862562444697277570353857512909352896131571712x35
+ 557562963539983202950691185462801065540725088264192x34
+ 1577030598282891711627871845517571153503680865904640x33
- 4031355006407679581510340088237124629945702313908224x32
+ 9320359108770148566726830291020142357508994547003392x31
- 19498017707740074863105993611122477732885838046508032x30
+ 36917622407933007707591207527855087843401265870534656x29
- 63267096157303351735591162217056900841844882144447488x28
+ 98117343437835396610929618461689230673920942360812032x27
- 137647138568449687304093633523852876065348682650976768x26
+ 174573112145310071129807575580039339572697009775656448x25
- 199992586141058806412294522911173007780459799455329024x24
+ 206734187166780667367389033001118161693782211050257408x23
- 192574938664678688530901838672535874100945425617703424x22
+ 161393923381751121129281862262305305700271471210142592x21
- 121467156951310355803305324565969723316823132273061248x20
- 81914307091912289239727046172116727761301978566859776x19
- 49371842718027401767568644806880416717266225110452672x18
+ 26517437794377160931097351789646070815460827122864384x17
- 12648231413882660861286679791033484384912047575614272x16
+ 5336484662604667578631882756675639804489817243827296x15
- 1982516704261427164713638931135138783194891086018464x14
+ 645059377822701742103935191747246560044012627107808x13
- 182682974642336401178456487920641420843900476505424x12
+ 44701978223308224633810906714599616362128447465632x11
- 9369170023670130301142557162275050714450300870432x10
+ 1664453923300763991366876751622333731454433911032x9
- 247450931086264938045712250664343672185343595304x8
+ 30301004268689512113386967850861704617367658320x7
- 2995034372940790154197150337328967090818065532x6
+ 232708537025651093654259832996385499856374072x5
- 13707236139496964340620953393151765582638388x4
+ 580782654055874340787700938178662406300926x3
- 16292257846517878837094859211571218061502x2
+ 260117200922134949258306409122197197946x
- 1638075168736052964113158952499236561.
- B(10)
- P = 14635757607000735744000000000x60
+ 2861715112497504898252800000000x59
+ 274943969090775430966804480000000x58
+ 17068281223043461657325993984000000x57
+ 767287718430620548958613248409600000x56
+ 26593123573273611623178374280642560000x55
+ 739240675412294047489303864737267712000x54
+ 16935167653330622995755712112714003251200x53
+ 326095803806505108284100359901038992424960x52
+ 5357191014616576523392303593701335424303104x51
+ 75966947740946554634950058941611847987494912x50
+ 938531719812983235443232940716123198681251840x49
+ 10178829092180843265695439239690585802790666240x48
+ 97518214203867427604096600707522395568418586624x47
+ 829621336333930213703092173156532653032269152256x46
+ 6294935860014800301566933739122157305954406760448x45
+ 42760416130140174414625321249641224257128389148672x44
+ 260864783169804030555281906484844315877596196765696x43
+ 1433164590469502429556328507135704002504202888675328x42
+ 7107197751564817284662358136064827080789739828150272x41
+ 31877989725466687445545471245326373474649022557847552x40
+ 129543119718765637104817677007452755915320911921676288x39
+ 477634908236491224561562728507575867873965530308149248x38
+ 1599784614652415422999513015127783357170721440745390080x37
+ 4872403163798730912946686636341339776184769301780103168x36
+ 13504784533437013789200225432496305394085904381558915072x35
+ 34084793818713770975839959595543023244790472770685239296x34
+ 78370272480681784494417049229122878411878328681346629632x33
+ 164200645552674795873154942417946428233203917835301027840x32
+ 313526373131064731655235302013214195970273880942177157120x31
+ 545532243270450260052616476368153018972914058591865929728x30
+ 864796055626920749048683896288732219386282445343442337792x29
+ 1248478634216103755955746803235379062408968913248363479040x28
+ 1640496989789200714009360418030439339028111701203040075776x27
+ 1960524467645976689272497366929311566226964388699262943232x26
+ 2128954263609478729765531027646435696959039559510593110016x25
+ 2098295963082473871752331797148145494274479643469891502080x24
+ 1874524173008117040880151427018780610012438354864814161920x23
+ 1515506598101378134036102950638005385519171115087483109376x22
+ 1106821851514361503444788409369920646993848394485348696064x21
+ 728689131534252108873099205238952205957484429377391296512x20
+ 431430120577839412226635972458454968683201605912329453568x19
+ 229082438414199474826702699700313311142410875268407230464x18
+ 108749124987534097236842856594610005561981576091600945152x17
+ 45989206466649145690216370016162199490544914108063612928x16
+ 17254296614707669095571650797029589694905604233641033728x15
+ 5716035123867046921679052366827435837495030353746788352x14
+ 1662916961207961644455247736610711932926165683744079872x13
+ 422136554356421413674379706136517275553004278087270400x12
+ 92807919905643649786010134585735055590256875745820672x11
+ 17514535463222622640662079801206641233028701967638528x10
+ 2806989448574866421248432603767857312404472260419584x9
+ 377074252440858304071244976144561895129908827849728x8
+ 41771276621016612682679851396992869345740084177920x7
+ 3737357394805943943743197930616926848662752151040x6
+ 262794113865459730462427194221876008085866568192x5
+ 13988711517879796391402873654850171597954470528x4
+ 533967443850703183450593313160551320351736960x3
+ 13419881266613014817006005535028255355316544x2
+ 190183880528759758990508532345771001310144x
+ 1043718457971658827739065564585623235937.
- C(1)
- Q = x3 - x2 + 5x + 1,
P = 45x3 + 273x2 + 791x + 427.
- C(2)
- Q = x6 - 3x5 + 4x3
+ 3x2 - 9x - 8,
P = 175x6 + 2430x5 + 19017x4
+ 64068x3 + 96849x2 + 65502x + 14103.
- C(3)
- P = 4465125x10 + 114448950x9
+ 1717178265x8 + 13590342216x7
+ 64780856250x6 + 190045721668x5
+ 345207245482x4 + 376373703112x3
+ 232122416801x2 + 72368288630x + 8271649661
- C(4)
- P = 46414974375x15 + 1935912990375x14
+ 47642771951775x13 + 679387553811135x12
+ 6409498796289459x11 + 41441755477203315x10
+ 186714655833929691x9 + 592398220222283579x8
+ 1329789279364354133x7 + 2109332508307537877x6
+ 2342269666378397405x5 + 1783536720101601725x4
+ 896749201669458449x3 + 278709535385588177x2
+ 47252708713917161x + 3194956880159369.
- C(5)
- P = 33990957x20 + 2066170260x19
+ 74666366110x18 + 1631856979620x17
+ 24611630588625x16 + 266019245095440x15
+ 2109653107162920x14 + 12489093935915280x13
+ 55920663405670730x12 + 190918816431017880x11
+ 498880666211503668x10 + 997491312345752120x9
+ 1519957436433127770x8 + 1751012290740378960x7
+ 1506000289549705640x6 + 949210838451943632x5
+ 426524139389956425x4 + 131002511542763380x3
+ 25680204113378910x2 + 2831323762830660x + 128953327629845.
- C(6)
- P = 12714083695698776015625x28
+ 1120748524109664262312500x27
+ 57932563572251162785856250x26
+ 1892177466425428784158462500x25
+ 43909208220618548969489251875x24
+ 758092200911073737253972545400x23
+ 10025138329822562476810869601380x22
+ 103714482141650900394345114152568x21
+ 852821642617789924119326347588401x20
+ 5638872391161332880603516326983260x19
+ 30236126600372747891562842066146278x18
+ 132302811233171030834279826571062348x17
+ 474549947715716153182346460436658627x16
+ 1399561783623525706921294566000827344x15
+ 3399709827516384207967064492097608952x14
+ 6804503836358553175105355044194027344x13
+ 11210406695245754458208568294556851475x12
+ 15164600636056464602949538789069164204x11
+ 16772766334005620201864939469243783974x10
+ 15075106075062159481220712426915177340x9
+ 10916068272134699647500006566594835585x8
+ 6294437221399060971901979957863369528x7
+ 2845051570593642241155761065561201508x6
+ 986558046370922512642081687153003704x5
+ 254655169100199472612495154296938163x4
+ 46810377310770276273113256289006148x3
+ 5712327818280188039476572427110714x2
+ 407530111261671567203245308353428x
+ 12528354714335602493796372103577.
- C(7)
- P = 438120013555654794702228515625x36
+ 52159336887503771380534767187500x35
+ 3620498455879214210677300768593750x34
+ 162403784641633545880539075901687500x33
+ 5264661149047477361323993504975340625x32
+ 129472760905531572410213222525202540000x31
+ 2492043588540203828904082500509491002000x30
+ 38388362414885821861871547859243945768800x29
+ 481182170246522749896746263006865892202260x28
+ 4969354620272733638376380165277357773617296x27
+ 42694952682059085248499417139591106649186024x26
+ 307549710995946552875807151256795690482347664x25
+ 1869292905817131057233263721850134407687841892x24
+ 9636542077913459701466058149810305897309244832x23
+ 42312238090549463600079425961098676018940492272x22
+ 158756811211009412422407684018072611385175599904x21
+ 510238603086453895162310927438419013737786355742x20
+ 1407011552533420257353009232922961339099482368456x19
+ 3331859964694969468079529214568852878970494207364x18
+ 6776470668203057547206859796942329839074785541128x17
+ 11830248005146609339758302737302218860919499842430x16
+ 17704262057551745876140880144164521007871901744672x15
+ 22663733694067693074628159528522649255713444397040x14
+ 24743143798661045591190384349571775250117550755488x13
+ 22946945298691782878446364260445408179250108380708x12
+ 17985660359193825201063775954487985522458754116112x11
+ 11837372398823589011637736861725585870069830635752x10
+ 6489041478426275875049465966382694044087742642448x9
+ 2932547999370610138970054468937012986506120886868x8
+ 1078380580802221455107075866627705056924457236576x7
+ 317258260050695747451310334711593582837834537104x6
+ 73016343806481444988042907345096990657726236896x5
+ 12746562667964817552151149773179726206084591489x4
+ 1614050192081379062637308334693453719175566188x3
+ 138195294992886800605459048143406833605584470x2
+ 7049731770073321764690143539043276665428876x
+ 158320694832222900012097032628451757776249.
- C(8)
- P = 19978981326387509765625x42
+ 2983185126665458558593750x41
+ 261140441674339488589453125x40
+ 14895541280747211525065625000x39
+ 619928588824336051802775406250x38
+ 19746431081104682830862599812500x37
+ 496931097760175099404038922726250x36
+ 10104553672895574567257607215793000x35
+ 168763551357708334525933574330774625x34
+ 2343769314924275723009257850055024030x33
+ 27327311635707106216349418952703586629x32
+ 269586130758399823281680276840789379872x31
+ 2264592996585577879119155922986124134744x30
+ 16284308646074667643684714843315004084720x29
+ 100678850545126535517925780418346313469336x28
+ 537130768625113392337031272077559663440800x27
+ 2480363896643816675438666427111182437483762x26
+ 9939063824429909070224720213589346503547660x25
+ 34632130649757908618507525522506211386456810x24
+ 105110805998395589428492727213862366094422320x23
+ 278231503795299031447078051209411310696920092x22
+ 642887124127653808431677180360346076125745400x21
+ 1297256648380934159482155037810595472640663516x20
+ 2286002792191346688643833593936669898338330416x19
+ 3516206336487619227598254496187972651841395146x18
+ 4716062671826499738665222453827978526944876044x17
+ 5506898780728422364162513440339108785882682258x16
+ 5585994174003805145599616210217779076226756512x15
+ 4907952137392685729209804527599765010041353240x14
+ 3721371244109326434209927557392504742264326640x13
+ 2423852958766756705861796591798003533876481752x12
+ 1348454696316409948521633268660324150388416288x11
+ 636280360180638678683209907648708802449087029x10
+ 252457646266680061053087282606004655589333022x9
+ 83328746480937673884206932856164556224051377x8
+ 22573914153763372836973954116827233325352552x7
+ 4933071235602063533458628950369562648627658x6
+ 850061838049804629499098294258033614956948x5
+ 111973939498654066613232275562288819911242x4
+ 10781172185433712334113804061493625143976x3
+ 707362324830242750821335230343132326581x2
+ 27879339953976590435166859062127141462x
+ 488342166322371232909880230533140041.
- C(9)
- P = 3943988517696329309474874414036059896739501953125x55
+ 778311923110674963236504321809947069645837158203125x54
+ 88521665310388080821128397451986702836385689306640625x53
+ 6686991597713205367021085074111958316398055809619140625x52
+ 372641574642624233763962527496220943439328473636560546875x51
+ 16124880337696730645648527983558550437350539946557416796875x50
+ 560014154423120530661496406913754271430408755528615290234375x49
+ 15978615430187676465988665223784630517917750901284065776234375x48
+ 381084810566558809659509254874856779232837286021618225662543750x47
+ 7698280504231519249876745237539002318530166892990040995053963750x46
+ 133111821381452473891242341153370497197382910149864700230367468750x45
+ 1987074663214034291989740864788129009310269997082285944739021102350x44
+ 25792046498356966293147593767828052053166243802743830665267602955570x43
+ 292850217672353760894509359054892452380945657793971075078818568862482x42
+ 2923619222156391543925396346245746575234037500775923930388325806267930x41
+ 25776597802872637845957390671796400755690111467562319213205912698806426x40
+ 201472502452438427787488450193534099322309620306910842966130946534890359x39
+ 1400652501436078810474567349912176713271409254397821099492187261182496295x38
+ 8686050334554010369362786776707770402463833590529078476795305296513316251x37
+ 48170496991258275498391149642575854976464196906187567841665699910019520123x36
+ 239414274307765658042780881799097354300549483109016797109083193325075633105x35
+ 1068413179313362889992274443312036048064954013894980724833327692405704752385x34
+ 4287814773025326266291417954225831822418149921229752655772299133868563527445x33
+ 15495764552272754605450375707287025946212812358102144519777688673280412101909x32
+ 50481788460369003605156275189980045978839363124320697188113853821160951260932x31
+ 148375703803697601745538956272427706378003036213636859845464359981796723573060x30
+ 393694965292990297040093338717700928652178252928609396675942807679393163414196x29
+ 943392711863977354736154491543373869539141474302917809162904270926562931963444x28
+ 2041892849291404929193252814646794469318665375289034644412994681691792436244524x27
+ 3991714971856941209438623784056175817657559326226597291525556766723912435449196x26
+ 7046219599935337399607836500579195566771614689465930988938386042105589040847388x25
+ 11225625074833297081425610004670032321151286497194033397324978855017606111677212x24
+ 16129121062391858147261960885315323374792674094403141862554089633600020132003331x23
+ 20880481716541195334871837785296508268190249580966945478191506089016970747526387x22
+ 24326133286386448309226527939876163883039669710707391243674913290757183994479895x21
+ 25466094980744234411614769057032238464071974194228146746918567792928793735944183x20
+ 23912903559330518439060098689690378788784754870230000029666716207815057458281517x19
+ 20098484668173596078629456910452535276496425582580201324654900186720722796027933x18
+ 15082555418352942398253074437396138126620857773772841428314236286848464070470337x17
+ 10076375561561334971892783543532763597425834001819964792120207142700848938216513x16
+ 5972815992777494749973546457430725158007831256768818441171913222517389941609750x15
+ 3128834877467709222509883654425438955499748358424221954364812822004495564659318x14
+ 1441815133475930355632725885349172716966301631184879585827004125402323843265950x13
+ 581310659414440101060887497078507226275076677683019991339409824678886684880350x12
+ 203753239862036592300698890035381368775920149169406019715099630366114072066178x11
+ 61616761543562395121724144396829980386607208979489841865280110288483383191394x10
+ 15930354344229279182010563900877932010889379053541041590880628158713706840362x9
+ 3482184908760173407631686843047113825376817868568663365963815175740588379562x8
+ 634725940515403047111777636601741146764186511197573189033805690166826304129x7
+ 94804837914445716818920104094546132350672770651965319198794693138080874577x6
+ 11341261078023732544244316088710980435428322902536173908288986155865925437x5
+ 1053402360466354870278414398289461563794297582871654068090911920041566301x4
+ 72653045799828251122928523910557125493397353259197144767539054780485095x3
+ 3470325051608917926388109769591785678814574252345836617237235396632631x2
+ 101293142985556017475649988344042219200453662149554823788707729870531x
+ 1339528345709395891100601544080319508719136732164912389838408109507.
IV.3.3 Remarques
a. Groupe de monodromie
Nous pouvons assez facilement calculer le groupe de monodromie
de ces arbres ; pour les arbres irréductibles
c'est le groupe alterné (pour A(k) et C(k) avec k pair)
ou le groupe symétrique (pour B(k) et les autres A(k) et C(k)).
Si nous notons GN le groupe engendré par
les deux permutations (1,2,...,N) et (1,2,3),
ce groupe est
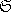 N.
si N est pair
et AN si N est impair.
Nous montrons ci-dessous que le groupe de monodromie
de tout Y-arbre irréductible contient GN,
et la signature
de
N.
si N est pair
et AN si N est impair.
Nous montrons ci-dessous que le groupe de monodromie
de tout Y-arbre irréductible contient GN,
et la signature
de  0
et
0
et  1
permet de conclure.
1
permet de conclure.
Pour les Y1,1,N-2,
la permutation 
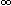 est un cycle de longueur N,
par exemple (1,2,...,N) et la permutation
est un cycle de longueur N,
par exemple (1,2,...,N) et la permutation
 02
est alors le cycle (1,2,3).
Pour les Y2,2,2k+1,
si
02
est alors le cycle (1,2,3).
Pour les Y2,2,2k+1,
si 
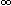 =
(1, 2, ... , 2k+5), alors
=
(1, 2, ... , 2k+5), alors
 02
est le cycle (1,3,5).
Comme la longueur de
02
est le cycle (1,3,5).
Comme la longueur de

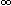 est impaire,
est impaire,

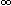 2 =
(1, 3, 5, ... ) est aussi un cycle de longueur 2k+5.
On voit d'ailleurs que cette construction ne marche pas
avec les Y2,2,2k, pour lesquels la longueur du
cycle de
2 =
(1, 3, 5, ... ) est aussi un cycle de longueur 2k+5.
On voit d'ailleurs que cette construction ne marche pas
avec les Y2,2,2k, pour lesquels la longueur du
cycle de 
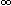 est un nombre pair.
Ce sont des Y-arbres de type D
dont le groupe de monodromie est le carré du groupe
de monodromie de Y1,1,k.
est un nombre pair.
Ce sont des Y-arbres de type D
dont le groupe de monodromie est le carré du groupe
de monodromie de Y1,1,k.
b. Les arbres Y1,1,2k+1
Pour k < 13, le nombre premier 2 ne se ramifie pas
dans le corps des modules.
Cette particularité n'a pas de preuve élémentaire.
![]() et
et
![]() .
Les types des trois sommets de valence 1
forment un invariant Galoisien qui détermine
quatre familles d'arbres en Y.
Nous supposons que le sommet de valence 3 est de type
.
Les types des trois sommets de valence 1
forment un invariant Galoisien qui détermine
quatre familles d'arbres en Y.
Nous supposons que le sommet de valence 3 est de type
![]() et nous comptons le nombres d'arbres de chaque type
avec la formule du paragraphe II.3.4.
Ici, k est un entier naturel quelconque.
et nous comptons le nombres d'arbres de chaque type
avec la formule du paragraphe II.3.4.
Ici, k est un entier naturel quelconque.
![]() de degré assez élevé, ce qui permet de tester nos algorithmes.
de degré assez élevé, ce qui permet de tester nos algorithmes.
![]() de valence 3 en 0, le sommet
de valence 3 en 0, le sommet ![]() de valence 1 en 1,
et le polynôme P est le polynôme minimal de la
somme des deux sommets
de valence 1 en 1,
et le polynôme P est le polynôme minimal de la
somme des deux sommets ![]() de valence 1.
de valence 1.
![]() de valence 3 en 0, le sommet
de valence 3 en 0, le sommet ![]() de valence 1 en 1,
et le polynôme P est le polynôme minimal de la
somme des deux sommets
de valence 1 en 1,
et le polynôme P est le polynôme minimal de la
somme des deux sommets ![]() de valence 1.
de valence 1.


![]() N.
si N est pair
et AN si N est impair.
Nous montrons ci-dessous que le groupe de monodromie
de tout Y-arbre irréductible contient GN,
et la signature
de
N.
si N est pair
et AN si N est impair.
Nous montrons ci-dessous que le groupe de monodromie
de tout Y-arbre irréductible contient GN,
et la signature
de ![]() 0
et
0
et ![]() 1
permet de conclure.
1
permet de conclure.
![]()
![]() est un cycle de longueur N,
par exemple (1,2,...,N) et la permutation
est un cycle de longueur N,
par exemple (1,2,...,N) et la permutation
![]() 02
est alors le cycle (1,2,3).
Pour les Y2,2,2k+1,
si
02
est alors le cycle (1,2,3).
Pour les Y2,2,2k+1,
si ![]()
![]() =
(1, 2, ... , 2k+5), alors
=
(1, 2, ... , 2k+5), alors
![]() 02
est le cycle (1,3,5).
Comme la longueur de
02
est le cycle (1,3,5).
Comme la longueur de
![]()
![]() est impaire,
est impaire,
![]()
![]() 2 =
(1, 3, 5, ... ) est aussi un cycle de longueur 2k+5.
On voit d'ailleurs que cette construction ne marche pas
avec les Y2,2,2k, pour lesquels la longueur du
cycle de
2 =
(1, 3, 5, ... ) est aussi un cycle de longueur 2k+5.
On voit d'ailleurs que cette construction ne marche pas
avec les Y2,2,2k, pour lesquels la longueur du
cycle de ![]()
![]() est un nombre pair.
Ce sont des Y-arbres de type D
dont le groupe de monodromie est le carré du groupe
de monodromie de Y1,1,k.
est un nombre pair.
Ce sont des Y-arbres de type D
dont le groupe de monodromie est le carré du groupe
de monodromie de Y1,1,k.