Pour utiliser une méthode numérique de résolution du système, nous devons trouver une première approximation du dessin, qui soit assez proche de la solution pour être dans la zone de convergence de l'algorithme de Newton. Comme on le voit dans [9] et dans le paragraphe IV.4.2, la géométrie d'un dessin a l'air de respecter une certaine régularité.
La généralisation des fonctions de Belyi sous la forme de différentielles de Strebel permet d'avoir une transformation continue d'un dessin vers un autre. En particulier, le dessin ci-dessous explique comment on peut raisonnablement supposer que le dessin de valences [25; 3 122; 9 82] est proche du dessin de valences [24; 3 121; 83] qui est lui-même un multiple de [6; 3 13; 23].

Le principe est donc d'utiliser les positions des points de ramification d'un dessin dont la structure en tant que graphe est proche du dessin que nous voulons calculer. Notre méthode, qui repose sur l'intuition de l'utilisateur, effectue des calculs de fonctions de Belyi de dessins de plus en plus compliqués, et se ressemblant.
Si on considère un dessin (de genre 0) comme un graphe plan, nous pouvons nous demander ce qui se passe si on supprime un sommet de ce graphe, en particulier si c'est un sommet de valence 1. On remarque ``expérimentalement'' que les positions des sommets éloignés sont presque inchangées.
Le procédé inverse, qui consiste à rajouter un sommet à une position bien choisie, pour avoir ainsi une estimation de la position des sommets d'un dessin plus gros, a donc de bonnes chances de marcher. En effet, c'est ainsi que je réussis à calculer les exemples du chapitre IV.
Ce sont des considérations locales qui vont nous permettre de savoir où placer le point supplémentaire. On prouve facilement que les angles formés par les arêtes du dessin autour d'un point de ramification sont égaux, car la réciproque de la fonction de Belyi est une racine n-ième. Quant à la distance des sommets voisins d'un autre sommet, elle dépend principalement de leur valence.
Dans un premier temps,
nous supposons que (localement au moins)
le dessin est un arbre.
Nous avons un sommet central et k
voisins, de valences (ni)i=1...k.
La distance du sommet numéro i
est environ ni / ![]() jnj.
Cette première estimation est assez
précise.
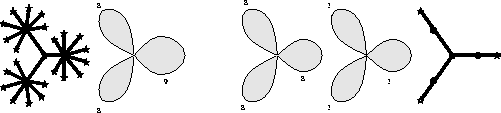
La figure IV.2 montre
deux exemples de familles d'arbres,
où on rajoute un sommet à chaque étape.
jnj.
Cette première estimation est assez
précise.
La figure IV.2 montre
deux exemples de familles d'arbres,
où on rajoute un sommet à chaque étape.
Dans un deuxième temps, nous étendons cette estimation au cas où un des sommets voisins est contigu à une face de valence 1, le dessin a une boucle. On peut appliquer la même estimation de distance, en considérant un poids wi au lieu de la valence ni de chaque sommet. On pose wi = ni - 1 pour le sommet d'où part la boucle et wi = ni + 1 pour les autres. Cette estimation est elle-aussi assez efficace.
En règle générale, nous pouvons considérer chaque sommet comme une charge répulsive de valeur wi, telle que wi croît si le nombre de sommets voisins croît, et décroît s'il y a des boucles de petite longueur.
Comme précisé en I.1.3, un tel calcul
n'est envisageable que si nous savons qu'un corps K
de définition du dessin est inclus dans un Qp connu.
Par exemple, Malle [29] a ainsi calculé un
polynôme ayant groupe de Galois M22.
Il fallait calculer un dessin défini sur
Q(![]() -11),
qui est inclus dans Q23.
Après recherche par bases de Gröbner des solutions modulo 23,
il utilise le lemme de Hensel pour avoir son résultat
dans Q23.
Comme
Q(
-11),
qui est inclus dans Q23.
Après recherche par bases de Gröbner des solutions modulo 23,
il utilise le lemme de Hensel pour avoir son résultat
dans Q23.
Comme
Q(![]() -11),
est de degré 2, il utilise les fractions continues pour trouver
une formule exacte du résultat. En degré supérieur à 2,
nous pouvons utiliser LLL.
-11),
est de degré 2, il utilise les fractions continues pour trouver
une formule exacte du résultat. En degré supérieur à 2,
nous pouvons utiliser LLL.
Dans le cas de revêtement ramifiés au dessus de quatre points, le déplacement des valeurs de ramification donne un revêtement dont la description numérique est proche. Si on réunit deux ramifications distinctes, les propriétés algébriques sont radicalement changées, mais l'aspect numérique reste proche.
Ici aussi l'intuition géométrique joue un rôle fondamental, mais dans ce cas elle peut s'appuyer sur des théorèmes. Matzat [34] par exemple a montré comment il est possible de décrire algébriquement la collision (ou l'éclatement) de deux valeurs de ramification. En pratique, cela signifie qu'on peut ne regarder que la monodromie du revêtement et en déduire celle du revêtement dégénéré.
Le passage par un revêtement ramifié au dessus de quatre points est utilisé par Matiyasevich [31] pour automatiser le calcul des fonctions de Belyi des arbres.
Il appelle polynôme quasi-généralisé de Tchebitchev
un polynôme ayant quatre valeurs critiques : -1, 1,
![]() et C,
avec -1 < C < 1 et tel qu'il existe un seul point critique
au dessus de C, de valence 2, noté w.
Les polynômes quasi-généralisés de Tchebitchev de degré N
définissent une famille de revêtements ramifiés au
dessus de quatre valeurs, dont les revêtements dégénérés
correspondent à tous les polynômes généralisés de Tchebitchev de degré N,
c'est-à-dire tous les dessins d'enfants de degré N qui sont des arbres.
et C,
avec -1 < C < 1 et tel qu'il existe un seul point critique
au dessus de C, de valence 2, noté w.
Les polynômes quasi-généralisés de Tchebitchev de degré N
définissent une famille de revêtements ramifiés au
dessus de quatre valeurs, dont les revêtements dégénérés
correspondent à tous les polynômes généralisés de Tchebitchev de degré N,
c'est-à-dire tous les dessins d'enfants de degré N qui sont des arbres.
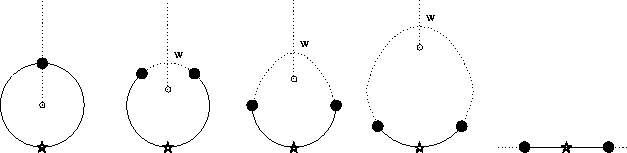
Matiyasevich effectue ainsi le calcul de tout arbre de degré N, en partant du polynôme généralisé de Tchebitchev 1 - 2xN qui correspond à l'étoile à N branches. La séquence de dessins ci-dessous montre la transformation d'un arbre en un autre, la valeur de C se déplaçant continument de -1 vers 1 :
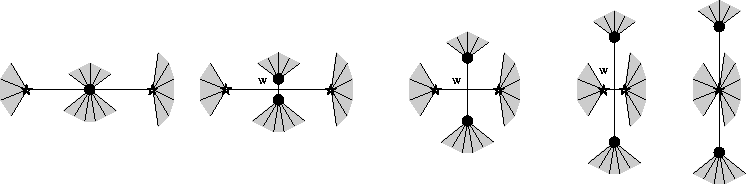
L'article de Matiyasevich peut facilement être généralisé
au calcul de n'importe quel dessin de genre 0 :
on définit les fonctions de quasi-Belyi comme ayant quatre
valeurs de ramification 0, 1, ![]() et C, de telle
sorte qu'il n'existe qu'un point critique, de valence 2,
au dessus du réel C.
Le déplacement de C entre 0 et 1 correspond aux dessins
ci-dessus, le déplacement de C entre 0 et
et C, de telle
sorte qu'il n'existe qu'un point critique, de valence 2,
au dessus du réel C.
Le déplacement de C entre 0 et 1 correspond aux dessins
ci-dessus, le déplacement de C entre 0 et ![]() au
dessin ci-dessous et change le nombre de faces du dessin.
au
dessin ci-dessous et change le nombre de faces du dessin.