I.1 Notions d'algèbre
Les fondements du calcul algébrique sont
les polynômes sur un anneau ou un corps.
On parle de géométrie lorsqu'on
considère les corps des réels R ou des
complexes C .
On parle d'arithmétique à propos des
rationnels Q et des corps de nombres.
Dans cette section
nous rappelons quelques définitions
élémentaires d'algèbre principalement.
Ensuite, nous présenterons les corps
de nombres, en faisant allusion à
leur interaction avec la géométrie,
par leurs plongements dans C
et les métriques sous-jacentes.
Nous esquisserons enfin le
lien entre géométrie et algèbre
qui se présente sous la forme
de variétés algébriques solutions
de systèmes polynomiaux,
et qui peut mener à la géométrie
algébrique.
Nous profitons de cette présentation
pour définir le groupe de Galois abolu
Gal(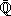 / Q),
mais cette notion ne sera utilisée
que dans le second chapitre,
sur les dessins d'enfants.
Son étude est l'une des
motivations du calcul explicite
des dessins.
/ Q),
mais cette notion ne sera utilisée
que dans le second chapitre,
sur les dessins d'enfants.
Son étude est l'une des
motivations du calcul explicite
des dessins.
I.1.1 Définitions
a. Anneau
On ne s'intéressera qu'aux anneaux unitaires intègres commutatifs.
On note A× le groupe multiplicatif des
éléments inversibles.
b. Idéal
Nous rappelons qu'un idéal I de A
est un sous-groupe de A stable par multiplication
par tout élément de A.
On note (F) l'idéal engendré par une partie
F de A, c'est-à-dire le plus petit
idéal contenant F. C'est la somme des
idéaux principaux xA pour x
élément de F.
Un idéal propre est un idéal différent de A.
Un idéal propre est maximal s'il n'est
contenu dans aucun autre idéal propre.
Un idéal premier est tel que
ab élément de I
implique a élément de I
ou b élément de I.
Le radical d'un idéal est
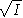 ,
c'est l'ensemble des x dont une puissance xn
est élément de I.
,
c'est l'ensemble des x dont une puissance xn
est élément de I.
La relation ``x-y élément de I''
est une relation d'équivalence qui
définit le quotient A / I,
qui est un anneau.
Cet anneau est intègre si I est premier,
c'est un corps si I est maximal.
c. Polynôme à une indéterminée
Un polynôme à coefficients dans un anneau A
est une application à support fini
P : N 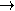 A ,
n
A ,
n 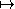 Pn.
On note P(X) =
Pn.
On note P(X) =
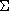 PnXn,
on dit que Pn est
le coefficient de Xn.
On note A[X]
l'ensemble des polynômes à coefficients dans A.
C'est un anneau, commutatif si A l'est.
PnXn,
on dit que Pn est
le coefficient de Xn.
On note A[X]
l'ensemble des polynômes à coefficients dans A.
C'est un anneau, commutatif si A l'est.
Le degré du polynôme est le plus petit d élément de
N 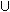 {-
{- }
tel que pour tout n > d, Pn = 0.
Par convention, le degré du polynôme nul est donc
-
}
tel que pour tout n > d, Pn = 0.
Par convention, le degré du polynôme nul est donc
- .
Le coefficient dominant d'un polynôme non nul est
Pd. S'il vaut 1, on dit que le polynôme
est unitaire.
.
Le coefficient dominant d'un polynôme non nul est
Pd. S'il vaut 1, on dit que le polynôme
est unitaire.
d. Polynôme à plusieurs indéterminées
Un polynôme à m indéterminées
est une application à support fini
P : Nm
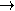 A ,
A ,

 P
P avec
avec  =
(
=
( 1, ... ,
1, ... ,
 m).
On note P(X) =
m).
On note P(X) =
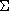 P
P X
X ou bien P(X1,...,Xm) =
ou bien P(X1,...,Xm) =
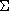 P
P 1,...,
1,..., m
X1
m
X1 1
...
Xm
1
...
Xm m.
Les polynômes à m indéterminées
à coefficients dans A forment un ensemble
noté A[X] ou
A[X1,...,Xm].
C'est un anneau isomorphe à
A[X1,...,Xm-1][Xm].
m.
Les polynômes à m indéterminées
à coefficients dans A forment un ensemble
noté A[X] ou
A[X1,...,Xm].
C'est un anneau isomorphe à
A[X1,...,Xm-1][Xm].
Le degré total du monôme
X est égal à
est égal à
 1 + ... +
1 + ... +
 m.
Son degré en Xm est
m.
Son degré en Xm est
 m.
On appellera support du polynôme
l'ensemble des
X
m.
On appellera support du polynôme
l'ensemble des
X tels que
P
tels que
P soit non nul
(et non l'ensemble des
soit non nul
(et non l'ensemble des
 comme on le fait parfois).
Le degré total d'un polynôme non nul est le
plus grand degré total des monômes de son support.
On dit qu'un polynôme est homogène
si tous les monômes de son support ont même degré total.
comme on le fait parfois).
Le degré total d'un polynôme non nul est le
plus grand degré total des monômes de son support.
On dit qu'un polynôme est homogène
si tous les monômes de son support ont même degré total.
e. Fonction polynomiale
Si A est commutatif,
on notera aussi P(x1,..., xm)
l'image par la fonction polynomiale associée à P
du m-uplet (x1,..., xm)
de Am.
C'est l'élément de A valant
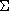 P
P 1,...,
1,..., m
x1
m
x1 1
...
xm
1
...
xm m.
m.
On peut remarquer que si E est une
algèbre (commutative) sur A, l'anneau A[X]
s'injecte dans E[X].
Le sous-ensemble de Em tel que
P(x1,..., xm) = 0
est noté VE(P). Cette notation sera utilisée
lorsque nous chercherons à résoudre des systèmes
d'équations polynomiales.
Les éléments de VE(P) sont appelés zéros
de P (dans Em).
Si m=1, on parle alors de racines.
f. Irréducibilité
L'anneau A[X] est factoriel si A l'est.
Si P peut se factoriser en polynômes de degré au plus 1,
on dit qu'il est scindé.
S'il n'admet pas de facteurs non triviaux,
on dit qu'il est irréductible.
Si x élément de A est une racine de P,
alors X-x divise P.
Si (X-x)n
est la plus grande puissance divisant P,
on dit que x est racine de P
avec multiplicité n.
g. Corps
On ne s'intéressera qu'aux corps commutatifs.
h. Extension algébrique
Un corps L est une extension du corps K si
L contient K. C'est alors un espace vectoriel sur
K, de dimension notée [L : K] et appelée
degré de l'extension.
Si L est distinct de K, c'est une extension propre.
Un élément x de L est algébrique sur K s'il
existe un polynôme non nul P de K[X]
tel que P(x)=0.
Une extension est algébrique si elle ne contient que des éléments
algébriques. Toute extension finie (i.e. de degré fini)
est algébrique.
Pour tout élément x algébrique sur K,
il existe un unique polynôme unitaire de degré minimal
annulant x, le polynôme minimal.
Ce polynôme est irréductible sur K.
On dit que x et y sont conjugués
s'il ont même polynôme minimal.
i. Transcendance
Soit une extension L de K.
Un élément x de L est transcendant
sur K s'il n'est pas algébrique.
Le degré [L : K] est alors infini.
Pour x1,..., xm éléments de L,
nous définissons l'anneau
K[x1,..., xm] inclus dans L,
qui est l'image de
K[X1,..., Xm]
par le morphisme qui à Xi associe xi.
Son corps des fractions
K(x1,..., xm)
est le sous-corps de L engendré par
K et x1,..., xm.
Le degré de transcendance de L
sur K est le plus petit m tel
que L soit une extension algébrique
d'un corps K(x1,..., xm).
Par exemple, si L est algébrique sur K,
son degré de transcendance est 0.
Autre exemple,
le degré de transcendance de R sur Q
est infini.
j. Polynôme caractéristique, trace et norme
Soit x élément de L une extension finie de K.
La multiplication par x
dans L peut être vue comme une application
linéaire de L en tant qu'espace vectoriel
sur K. Son polynôme caractéristique
est appelé polynôme caractéristique
de l'élément x dans l'extension L de K,
il est noté CarL/K(x).
Il est égal au polynôme minimal de x,
à la puissance [L : K(x)].
Nous écrivons CarL/K(x) =
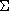 i(-1)d-i
sd-i(x)Xi,
où d = [L : K].
Le nombre sk(x), élément de K,
est appelé k-ième fonction symétrique
de x dans L / K .
La trace et la norme sont respectivement
TrL/K(x) = s1(x) et
NL/K(x) = sd(x).
i(-1)d-i
sd-i(x)Xi,
où d = [L : K].
Le nombre sk(x), élément de K,
est appelé k-ième fonction symétrique
de x dans L / K .
La trace et la norme sont respectivement
TrL/K(x) = s1(x) et
NL/K(x) = sd(x).
k. Clôture algébrique
Un corps K est algébriquement clos
s'il n'a pas d'extension algébrique propre.
Cela signifie que tout polynôme de K[X]
est scindé.
Une extension algébrique de K qui
est algébriquement close est appelée
clôture algébrique de K.
Les clôtures algébriques de K sont
isomorphes, on en choisit une qu'on
note 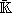 .
.
I.1.2 Corps de nombres
La théorie algébrique est plus facile à
appréhender lorsque le corps de base est
un corps primitif :
le corps des nombres rationnels Q
ou un corps premier Fp = Z / pZ.
Les systèmes algébriques que nous manipulerons
seront définis sur Q.
Un corps de nombres est une extension
K de degré fini du
corps Q des rationnels.
Les éléments d'un corps de nombres sont donc algébriques
sur Q. On les appelle les nombres algébriques.
a. Anneau des entiers
Il faut remarquer que Q est le corps des fractions de
l'anneau Z des entiers relatifs.
Si les coefficients du polynôme
minimal d'un nombre algébrique sont tous des entiers
relatifs, on dit que ce nombre est un entier algébrique.
L'ensemble des entiers algébriques de K est appelé l'anneau des
entiers, noté ZK.
C'est un Z-module libre de rang [K : Q],
dont les bases sont appelées bases intégrales de K.
On appelle contenu
d'un polynôme P de Q[X] le plus
grand rationnel positif c tel que c-1P
n'ait que des coefficients entiers.
Par abus de langage, on appelle aussi polynôme minimal
d'un nombre algébrique le quotient du polynôme
minimal par son contenu.
C'est ainsi le polynôme à coefficients
entiers, de degré minimal et de coefficient dominant
minimal positif, annulant ce nombre.
Les entiers algébriques sont alors les nombres dont
le polynôme minimal est unitaire.
b. Élément primitif
Le théorème de l'élément primitif affirme
que tout corps de nombres est isomorphe à un
quotient Q[X] / (P), où P est de
degré d = [K : Q].
Le polynôme P a au moins une racine
 dans K,
qui est par définition un élément primitif de K.
dans K,
qui est par définition un élément primitif de K.
La famille (1,  ,
,
 2, ...,
2, ...,
 d-1)
engendre K comme espace vectoriel sur Q,
ce qui signifie que K est égal à
Q[
d-1)
engendre K comme espace vectoriel sur Q,
ce qui signifie que K est égal à
Q[ ].
En revanche, l'anneau
Z[
].
En revanche, l'anneau
Z[ ]
n'est que rarement égal à ZK.
]
n'est que rarement égal à ZK.
Si  est un entier algébrique, on a
évidemment l'inclusion de
Z[
est un entier algébrique, on a
évidemment l'inclusion de
Z[ ]
dans ZK.
On note alors [ZK :
Z[
]
dans ZK.
On note alors [ZK :
Z[ ]]
l'indice du sous-groupe
Z[
]]
l'indice du sous-groupe
Z[ ]
dans ZK
(cf. paragraphe II.1.2.d.).
On l'appelle aussi indice de
]
dans ZK
(cf. paragraphe II.1.2.d.).
On l'appelle aussi indice de
 dans ZK.
Si d>2, il n'existe pas toujours d'élément d'indice 1,
par exemple dans Q[X] /
(X3 + X2 - 2X + 8).
dans ZK.
Si d>2, il n'existe pas toujours d'élément d'indice 1,
par exemple dans Q[X] /
(X3 + X2 - 2X + 8).
c. Plongements
Soit L est une extension algébriquement close
du corps de nombres K,
par exemple le corps C des nombres complexes
ou 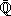 une clôture algébrique de Q.
Le polynôme minimal d'un élément primitif
une clôture algébrique de Q.
Le polynôme minimal d'un élément primitif
 de K,
irréductible de degré d sur Q, a d racines
distinctes
de K,
irréductible de degré d sur Q, a d racines
distinctes  i
dans L.
Chaque application
i
dans L.
Chaque application

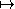
 i
donne un plongement de K dans L.
Ce sont les seuls.
Nous notons
i
donne un plongement de K dans L.
Ce sont les seuls.
Nous notons  i
ces plongements.
Dans le cas L = C, chaque plongement donne
ainsi une vision géométrique du corps K.
i
ces plongements.
Dans le cas L = C, chaque plongement donne
ainsi une vision géométrique du corps K.
On dit qu'un corps de nombres de degré d
est galoisien ou normal,
si les ensembles
 i(K)
sont égaux dans L.
C'est le cas si et seulement si le polynôme minimal
de
i(K)
sont égaux dans L.
C'est le cas si et seulement si le polynôme minimal
de  est scindé dans K, ce qui
signifie que
est scindé dans K, ce qui
signifie que  a d conjugués.
Le corps K est galoisien si, et seulement si,
il a d automorphismes distincts,
qui sont les
a d conjugués.
Le corps K est galoisien si, et seulement si,
il a d automorphismes distincts,
qui sont les  i
i  j-1.
Ces automorphismes forment un groupe qu'on note
Gal(K / Q).
Les automorphismes d'une clôture algébrique
j-1.
Ces automorphismes forment un groupe qu'on note
Gal(K / Q).
Les automorphismes d'une clôture algébrique
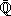 forment le groupe de Galois absolu
Gal(
forment le groupe de Galois absolu
Gal(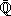 / Q).
/ Q).
d. Discriminant
Soit [K : Q] = d et une famille
(x1,..., xd) dans K.
Le déterminant de la matrice
(TrK / Q(xi
xj))i,j
est un nombre rationnel, dont le carré est
appelé discriminant de la famille,
noté d(x1,..., xd).
C'est aussi le nombre
[det( i(xj))]2.
i(xj))]2.
Le discriminant d'une base intégrale de K ne dépend
pas du choix de la base intégrale, et est donc appelé
discriminant du corps de nombres, noté d(K).
Deux corps de nombres distincts peuvent avoir même discriminant.
Par exemple Q[X] / (X4 + 2X3
+ 6X2 - 6)
et Q[X] / (X4 + 2X3
- 3X2 - 4X - 2)
ont pour discriminant -8640 et sont distincts.
Pour un polynôme irréductible P de degré d
dans Q[X] et de coefficient dominant c,
on note d(P) le discriminant du polynôme,
qui vaut
c2(d-1)
d(1,  ,
,
 2, ...,
2, ...,
 d-1)
où
d-1)
où  est une racine quelconque de P.
Si K = Q[X] / (P),
alors d(P) = d(K)f2
où f est appelé indice
du polynôme et est égal
à l'indice de
est une racine quelconque de P.
Si K = Q[X] / (P),
alors d(P) = d(K)f2
où f est appelé indice
du polynôme et est égal
à l'indice de  .
.
e. Représentation d'un corps de nombres
Le livre de Cohen [11]
est la référence sur les problèmes
algorithmiques en théorie des
nombres.
On peut représenter K comme sous-corps
d'un corps défini auparavant,
ou bien par un polynôme
tel que K est isomorphe à Q[X] / (P).
Plusieurs polynômes conviennent,
il est préférable d'en trouver
un de petite «taille»
(voir en particulier [11, p171]).
Le calcul d'une base intégrale et du
discriminant du corps est souvent
la première étape de l'étude
d'un corps de nombres.
Des algorithmes le permettent,
mais le temps de calcul est
souvent impraticable.
f. Représentation d'un nombre algébrique
Si ce nombre est dans un corps K connu,
dont on connaît une base sur Q (une base
intégrale par exemple) on utilise ses coordonnées
dans cette base.
Nous aurons besoin de faire des opérations
dans un corps de nombres inconnu a priori.
Il est donc naturel de représenter un nombre
par son polynôme minimal, et d'effectuer
les opérations de
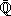 à l'aide de calcul de résultants de polynômes
[11, pp156-159].
Mais cette représentation
ne distingue pas les nombres algébriques conjugués.
Pour y arriver, on utilise
en plus une approximation du nombre considéré.
à l'aide de calcul de résultants de polynômes
[11, pp156-159].
Mais cette représentation
ne distingue pas les nombres algébriques conjugués.
Pour y arriver, on utilise
en plus une approximation du nombre considéré.
I.1.3 Approximation d'un nombre algébrique
La méthode numérique que nous proposons dans la section
I.3
utilise des approximations de la solution du système algébrique.
Nous devons donc définir une distance entre les éléments
de 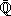 .
.
a. Corps métrique
Un corps K est un corps métrique
s'il est muni d'une fonction
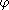 de K× dans R>0
telle que
de K× dans R>0
telle que
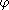 (x+y)
(x+y)
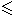
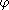 (x) +
(x) +
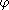 (y)
et
(y)
et 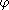 (xy) =
(xy) =
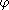 (x)
(x)
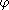 (y),
étendue sur K avec
(y),
étendue sur K avec
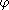 (0) = 0.
La fonction
(0) = 0.
La fonction 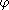 est appelée une valeur absolue.
Elle est ultramétrique
lorsque
est appelée une valeur absolue.
Elle est ultramétrique
lorsque
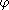 (x+y)
(x+y)
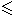 max(
max(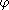 (x),
(x),
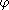 (y)).
Nous ignorerons la valeur absolue triviale où
(y)).
Nous ignorerons la valeur absolue triviale où
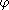 (K×)
= {1}.
(K×)
= {1}.
La distance entre x et y est
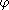 (x-y).
Une suite (xn) converge vers x si
la limite (réelle) de
(x-y).
Une suite (xn) converge vers x si
la limite (réelle) de
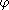 (xn-x) est 0.
Deux valeurs absolues sur K sont équivalentes
si elles définissent la même notion de convergence,
c'est-à-dire la même topologie.
Les valeurs absolues équivalentes à
(xn-x) est 0.
Deux valeurs absolues sur K sont équivalentes
si elles définissent la même notion de convergence,
c'est-à-dire la même topologie.
Les valeurs absolues équivalentes à
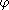 sont les
sont les 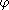
 ,
pour
,
pour  > 0.
Les classes d'équivalence de valeurs absolues
sont appelées places.
> 0.
Les classes d'équivalence de valeurs absolues
sont appelées places.
b. Valeur absolue p-adique
On appelle valuation discrète
 d'un corps K toute fonction v de
K dans Z
d'un corps K toute fonction v de
K dans Z 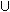 {-
{- } telle
que v(0) = -
} telle
que v(0) = - ,
v(K×) = Z,
v(xy) = v(x)+v(y)
et v(x+y)
,
v(K×) = Z,
v(xy) = v(x)+v(y)
et v(x+y)
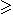 min(v(x), v(y)).
min(v(x), v(y)).

Sur tout corps K muni d'une valuation discrète v,
on construit une valeur absolue associée comme suit :
on choisit un réel
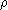 dans ] 0, 1[ ;
la valeur absolue de x est
|x|v =
dans ] 0, 1[ ;
la valeur absolue de x est
|x|v = 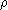 v(x).
Cette valeur absolue est ultramétrique.
v(x).
Cette valeur absolue est ultramétrique.
Soit  un idéal premier
de l'anneau des entiers ZK,
on définit la valuation
un idéal premier
de l'anneau des entiers ZK,
on définit la valuation
 -adique
sur K qui à tout x de K× associe l'entier
v
-adique
sur K qui à tout x de K× associe l'entier
v (x)
tel que l'idéal principal (x) se décompose en
(x) =
(x)
tel que l'idéal principal (x) se décompose en
(x) =  v
v (x) a/b
où les idéaux a et b ne sont pas divisibles
par
(x) a/b
où les idéaux a et b ne sont pas divisibles
par  .
En particulier, si p est un entier premier,
la valuation p-adique sur Q donne
vp(x)
tel que
x = pvp(x) a/b
avec a et b non divisibles par p.
Ce sont des valuations discrètes.
Les valeurs absolues associées sont notées
|·|
.
En particulier, si p est un entier premier,
la valuation p-adique sur Q donne
vp(x)
tel que
x = pvp(x) a/b
avec a et b non divisibles par p.
Ce sont des valuations discrètes.
Les valeurs absolues associées sont notées
|·| et |·|p.
et |·|p.
c. Places de Q et de ses extensions
Si on choisit un plongement
 de K dans C,
le module des nombres complexes est une valeur
absolue de K, qu'on note
|·|
de K dans C,
le module des nombres complexes est une valeur
absolue de K, qu'on note
|·| .
Pour les rationnels, c'est la valeur absolue usuelle.
.
Pour les rationnels, c'est la valeur absolue usuelle.
Toutes les valeurs absolues sur K sont équivalentes à
une valeur absolue  -adique
(places finies) ou à une valeur absolue
|·|
-adique
(places finies) ou à une valeur absolue
|·| .
(places infinies).
.
(places infinies).
d. Complétion
Soient K un corps métrique et x un élément de K.
Si l'élément
 est à une distance au plus
est à une distance au plus
 de x, on dit
que
de x, on dit
que  est
une approximation à
est
une approximation à  près de x.
Si nous avons une suite
(
près de x.
Si nous avons une suite
( n)
et un réel
n)
et un réel
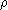 dans ] 0, 1[
tels que tout
dans ] 0, 1[
tels que tout
 n
est une approximation à
n
est une approximation à
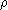 n
près des
n
près des
 k
pour k > n,
il est légitime de considérer que cette suite
converge vers une certaine valeur.
On dit qu'un corps métrique K est
complet si toutes ces suites (dites de Cauchy)
convergent dans K.
k
pour k > n,
il est légitime de considérer que cette suite
converge vers une certaine valeur.
On dit qu'un corps métrique K est
complet si toutes ces suites (dites de Cauchy)
convergent dans K.
Le complété de Q pour
|·| est l'ensemble des nombres réels R.
La clôture algébrique de R est le corps (complet)
des nombres complexes. C'est aussi le complété de
est l'ensemble des nombres réels R.
La clôture algébrique de R est le corps (complet)
des nombres complexes. C'est aussi le complété de
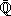 pour ses places infinies.
pour ses places infinies.
Les complétés de Q pour les valeurs absolues p-adiques
sont les corps p-adiques Qp.
Les complétés des corps de nombres pour les places finies
sont des extensions finies de Qp.
Leur clôture algébrique
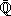 p
n'est pas complète.
On appelle Cp le complété de
p
n'est pas complète.
On appelle Cp le complété de
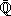 p,
qui est lui aussi algébriquement clos.
p,
qui est lui aussi algébriquement clos.
e. Approximation d'un rationnel dans la métrique usuelle
Soit x un réel. Soient deux entiers N > 1 et k.
Il existe un nombre de la forme
 = A N-k
où A est un entier relatif tel que
| x-
= A N-k
où A est un entier relatif tel que
| x- |
|
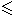 N-k.
On dit que
N-k.
On dit que  est une approximation à k décimales
en base N du nombre x.
Si x est le rationnel a / b, on calcule A comme
quotient euclidien de a Nk par b.
est une approximation à k décimales
en base N du nombre x.
Si x est le rationnel a / b, on calcule A comme
quotient euclidien de a Nk par b.
f. Approximation d'un rationnel dans une métrique p-adique
Soit x dans Qp. Soit un entier relatif k.
Il existe un entier relatif
 tel que vp(x-
tel que vp(x- )
)
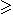 k,
c'est-à-dire
| x-
k,
c'est-à-dire
| x- |p
|p
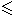
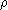 k.
On dit que
k.
On dit que  est une approximation p-adique
de précision k.
Si x = pvp(x)
a / b,
on calcule
est une approximation p-adique
de précision k.
Si x = pvp(x)
a / b,
on calcule  comme suit :
comme suit :
- lorsque vp(x)
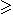 k,
k,
 = 0,
= 0,
- lorsque vp(x)
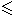 k,
k,
 =
pvp(x)
(a / b mod pk-vp(x)).
=
pvp(x)
(a / b mod pk-vp(x)).
g. Approximation d'un nombre algébrique dans C
Le corps C est une extension de R de degré 2.
Tout nombre complexe peut donc s'écrire
sous la forme a+ib avec a et b réels.
Étant donné un plongement
de 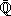 dans C,
nous pouvons approcher tout nombre algébrique
par un couple d'approximations de réels.
dans C,
nous pouvons approcher tout nombre algébrique
par un couple d'approximations de réels.
L'inconvénient de ce type d'approximation est
que la précision est difficile à maîtriser.
Le calcul par intervalles (plusieurs milliers
de publications sur le sujet, d'après Neumaier
[35])
est une solution élégante aux problèmes de
précision,
mais nous nous contenterons de vérifier a posteriori
les résultats (algébriques) de nos calculs.
h. Approximation p-adique d'un nombre algébrique
Le corps Cp est de degré infini sur Qp.
La clôture algébrique
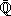 p
est elle aussi de degré infini sur Qp.
Nous ne pouvons donc pas approcher les nombres algébriques
aussi simplement qu'avec la métrique usuelle.
p
est elle aussi de degré infini sur Qp.
Nous ne pouvons donc pas approcher les nombres algébriques
aussi simplement qu'avec la métrique usuelle.
Cependant, pour tout n fixé, il y a un nombre fini
d'extensions de Qp de degré n.
Il existe donc une famille finie
(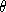 i)
dans
i)
dans 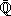 p
telle que tout élément algébrique sur Qp de
degré au plus n soit une combinaison linéaire
des
p
telle que tout élément algébrique sur Qp de
degré au plus n soit une combinaison linéaire
des 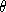 i
à coefficients dans Qp.
Mais cet ensemble n'est pas stable par multiplication,
il est donc impossible de s'en servir pour
faire des calculs approchés.
i
à coefficients dans Qp.
Mais cet ensemble n'est pas stable par multiplication,
il est donc impossible de s'en servir pour
faire des calculs approchés.
En revanche, pour tout corps de nombres K, il existe
une infinité de p tels que K
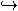 Qp
(Tchebotarev).
Si K = Q[X] / (P),
ce sont les p tels que P ait au moins une racine
modulo p.
Pour un tel p, on peut faire des calculs
approchés dans la métrique p-adique.
Qp
(Tchebotarev).
Si K = Q[X] / (P),
ce sont les p tels que P ait au moins une racine
modulo p.
Pour un tel p, on peut faire des calculs
approchés dans la métrique p-adique.
I.1.4 Système algébrique
Nous donnons les définitions qui
nous sont nécessaires.
Le livre de Fulton [21] donne
une présentation agréable des bases
de la géométrie algébrique,
nettement plus complète
et très lisible.
a. Espace affine, projectif
Pour un corps K, nous notons Am(K)
l'espace affine Km de dimension m.
Les zéros dans K d'un polynôme de
K[X1,..., Xm]
sont donc éléments de Am(K).
Si P est un polynôme homogène, tout
multiple d'un zéro de P est aussi un zéro.
L'ensemble des zéros d'un polynôme homogène
est donc un ensemble de droites passant
par l'origine. Nous notons Pm(K)
l'espace projectif de dimension m,
qui est l'ensemble des droites de Km+1
passant par l'origine.
b. Variété algébrique
Nous appellerons système algébrique une famille F
= (fi)
de polynômes de K[X] = K[X1 ,
..., Xm].
On s'intéresse aux zéros simultanés de tous ces
polynômes, dans K ou dans
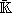 .
.
L'intersection des VK(fi)
(zéros sur K de fi)
est une partie de Am(K) qu'on appelle
un ensemble algébrique affine sur K.
L'intersection des
V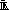 (fi)
est une variété algébrique (affine).
(fi)
est une variété algébrique (affine).
 Si V est une variété algébrique,
on note V(K) l'ensemble des points
K-rationnels de V, c'est-à-dire
V
Si V est une variété algébrique,
on note V(K) l'ensemble des points
K-rationnels de V, c'est-à-dire
V
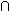 Am(K).
Am(K).
Lorsqu'on considère des polynômes homogènes de
K[X0 , ..., Xm],
l'ensemble des points annulant le système est une variété
projective, incluse dans l'espace projectif
Pm(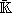 ).
).
c. Homogénéisation, déshomogénéisation
Dans la plupart des cas, il y a une correspondance
entre variétés affines et projectives et entre
polynômes de K[X1,..., Xm]
et polynômes
homogènes de K[X0 , ..., Xm].
Il existe cependant quelques pièges
que nous ne détaillerons pas,
dus à la présence de l'hyperplan à l'infini;
voir par exemple [21, p96 et suivantes].
Nous nous placerons donc dans le cas affine en
sachant qu'il aurait été possible
d'étudier le cas projectif.
Pour P de degré total d
dans K[X1 , ..., Xm],
nous notons P* le polynôme
homogène correspondant, qui vaut
P*(X0 , ..., Xm) =
X0d
P(X1/X0 , ...,
Xm/X0).
À l'inverse, la déshomogénéisation d'un polynôme
homogène P est le polynôme
P*(X1 , ..., Xm) =
P(1, X1 , ..., Xm).
d. Idéal engendré
Nous notons I = <fi>
l'idéal de K[X] engendré par les polynômes fi.
L'ensemble intersection des V(fi) ne dépend que
de l'idéal, on le note donc V(I).
Soit X une partie quelconque de l'espace affine Am.
L'ensemble de polynômes s'annulant sur X
est un idéal qu'on note I(X).
Le théorème des bases de Hilbert affirme
que tout idéal de K[X] est engendré
par un nombre fini de polynômes.
Cela signifie que nous pouvons nous
restreindre aux systèmes algébriques finis.
e. Corps de définition
On dit qu'une variété est définie
sur un corps K si elle admet un modèle sur K,
c'est-à-dire si l'idéal I(V) est engendré par
I(V)
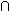 K[X].
K[X].
f. Composantes irréductibles
On dit qu'un ensemble algébrique V est irréductible
s'il n'est pas la réunion d'ensembles algébriques
plus petits.
Cette condition est vérifiée si et seulement si l'idéal I(V)
est premier.
Tout ensemble algébrique se décompose de façon unique
en la réunion d'un nombre fini
d'ensembles algébriques irréductibles
(dont aucun n'est inclus dans un autre),
ses composantes irréductibles.
g. Fonctions rationnelles
Si V est une variété irréductible définie sur K,
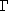 (V) =
K[X1 , ..., Xm] / I(V)
est un anneau intègre, qu'on appelle
anneau des coordonnées
ou anneau des fonctions régulières de V.
Il peut être identifié avec l'anneau
des fonctions polynomiales sur V.
(V) =
K[X1 , ..., Xm] / I(V)
est un anneau intègre, qu'on appelle
anneau des coordonnées
ou anneau des fonctions régulières de V.
Il peut être identifié avec l'anneau
des fonctions polynomiales sur V.
Son corps des fractions K(V)
est le corps des fonctions rationnelles.
h. Systèmes équivalents
On dit que deux systèmes (fi) et (gi)
sont équivalents si et seulement s'ils
ont la même solution. C'est en particulier
le cas si <fi> = <gi>.
Cependant, la réciproque est fausse :
V(I) = V(J)
n'implique pas I = J.
Un contre-exemple est I = <X>
et J = <X2>.
Sur un corps algébriquement clos,
le théorème des zéros de Hilbert
(souvent appelé Nullstellensatz)
donne le critère
V(I) = V(J) si, et seulement si,
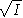 =
=
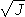 .
.
i. Dimension de la solution
Soit V une variété irréductible sur un corps K.
Si nous considérons le corps K(V)
des fonctions rationnelles sur V,
on appelle dimension de V son degré
de transcendance sur K.
Une variété de dimension 0
est un ensemble fini de points.
On appelle courbe algébrique
les variétés de dimension 1.
Une surface est une
variété de dimension 2.
j. Résolution d'un système algébrique
L'objectif de la résolution du système peut être :
- savoir tester si un polynôme f est élément de I.
- trouver un ou plusieurs zéros du système, quelques
éléments de V
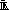 (I).
(I).
- connaître le nombre d'éléments de V
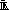 (I).
(I).
- calculer les composantes irréductibles de V
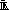 (I),
leur dimension.
(I),
leur dimension.
k. Exemple de système, pour un dessin très simple
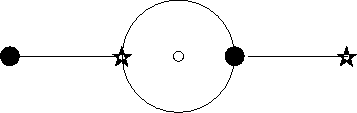
Figure I.1: Exemple de dessin, de valences [31,31,31]
On cherche la fonction de Belyi
du dessin de la figure I.1,
c'est-à-dire une fraction rationnelle
 ,
telle que la préimage
,
telle que la préimage
 -1([0, 1])
dessine le graphe de la figure.
Le système correspondant
est défini par
(cf. chapitres II
et III) :
-1([0, 1])
dessine le graphe de la figure.
Le système correspondant
est défini par
(cf. chapitres II
et III) :
(x + pa)3 (x + pb)
= 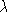 x +
(x + qa)3 (x + qb).
(égalité I.1)
x +
(x + qa)3 (x + qb).
(égalité I.1)
La variété solution a deux composantes :
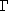 '' de dimension 2 '' de dimension 2
|
| 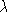 = 0, = 0,
| pa = qa,
| pb = qb;
|
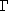 ' de dimension 1 ' de dimension 1
|
| 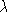 =
-16 pa3, =
-16 pa3,
| pa + qa =
pb + qb = 0,
| 3pa + pb = 0.
|
Si on élimine la première composante (en imposant
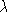 non nul,
par exemple en rajoutant
une inconnue
non nul,
par exemple en rajoutant
une inconnue 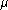 et l'équation
et l'équation 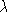
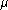 = 1)
et si on fixe l'échelle du dessin (en rajoutant
l'équation pa + pb = 2)
le système obtenu a une unique solution :
= 1)
et si on fixe l'échelle du dessin (en rajoutant
l'équation pa + pb = 2)
le système obtenu a une unique solution :
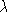 = 16, = 16,
| 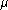 = 1/16, = 1/16,
|
| pa = -1,
| pb = 3,
| qa = 1,
| qb = -3.
|
L'égalité (I.1) est donc
(x - 1)3 (x + 3)
= 16 x +
(x + 1)3 (x - 3),
dont on déduit
 =
(x - 1)3 (x + 3) / 16 x.
=
(x - 1)3 (x + 3) / 16 x.
l. Exemple pour un dessin plus élaboré
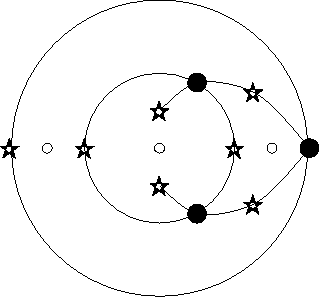
Figure I.2: Exemple de dessin moins simple,
de valences [1 42 3, 43, 25 12]
Le système correspondant au dessin de la figure I.2
(voir aussi § IV.4.3)
se construit à partir de l'égalité ci-dessous,
plus quelques considérations supplémentaires :
(x3 + pa x2
+ pb x + pc)4 =
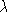 x3
(x2 - x + ra)4
x3
(x2 - x + ra)4
+ (x5 + qa x4
+ qb x3
+ qc x2
+ qd x + qe)2
(x2 + qf x + qg)
La variété solution qui nous intéresse est de dimension 0,
elle a quatre éléments conjugués dans le corps de nombres
Q[X] / (X4 - 2X3
- 2X + 1).
Si  est une racine de X4 - 2X3 - 2X + 1,
on a :
est une racine de X4 - 2X3 - 2X + 1,
on a :
- pa = ( 19507
- 3072
 - 29052
- 29052  2
+ 9976
2
+ 9976  3
) / 7678
3
) / 7678
- pb = ( -57446893
+ 36552960
 - 78891720
- 78891720  2
+ 40777808
2
+ 40777808  3
) / 58951684
3
) / 58951684
- pc = ( 763448412011
+ 69993771648
 - 1206701651460
- 1206701651460  2
+ 300422694344
2
+ 300422694344  3
) / 4978941327272
3
) / 4978941327272
- ...
- ra = ( 1541977
- 1470816
 + 12130864
+ 12130864  2
- 4799104
2
- 4799104  3
) / 16077732
3
) / 16077732
-
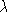 = ( -2009543040
+ 223727616
= ( -2009543040
+ 223727616  + 2094239232
+ 2094239232  2
- 718792704
2
- 718792704  3
) / 56206799
3
) / 56206799
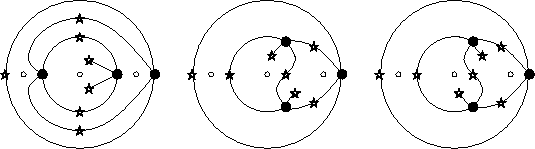
Figure I.3:
Les conjugués du dessin de la figure I.2.
![]() / Q),
mais cette notion ne sera utilisée
que dans le second chapitre,
sur les dessins d'enfants.
Son étude est l'une des
motivations du calcul explicite
des dessins.
/ Q),
mais cette notion ne sera utilisée
que dans le second chapitre,
sur les dessins d'enfants.
Son étude est l'une des
motivations du calcul explicite
des dessins.
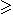 k,
k,


