II.1 Introduction aux dessins

II.1.1 Présentation informelle

a. Dessins dans le plan 

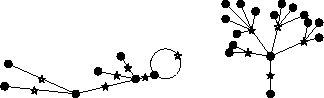
Dans le plan (R² ou C) nous plaçons un nombre fini de points de deux types, et nous traçons de lignes (ne se croisant pas) reliant deux points de types différents. Ceci est un dessin marqué de genre 0, représenté par une carte plane bipartite. Par exemple le bonhomme et la fleur de Leila ci-dessous.

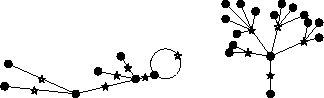
Si nous déformons ce dessin dans le plan, sa structure combinatoire est conservée. De cette description combinatoire, on peut déduire une description algébrique. C'est la correspondance de Grothendieck.

Il n'y a qu'une façon (à similitude directe près, ou échange des types des sommets) de tracer ce dessin dans le plan, qui corresponde à cette description algébrique. Grâce à des petits dessins, nous avons une façon élémentaire de représenter des objets algébriques qui peuvent être très complexes.

b. Préimage de [0,1] par une fonction méromorphe

La préimage d'un segment par une fonction méromorphe est la réunion de plusieurs segments. On appelle valeurs critiques de les images des racines de '. La préimage d'un segment par ne peut avoir de points multiples qu'en une racine de '.

Si nous choisissons une fonction méromorphe sur une surface compacte, par exemple la sphère C {} , la préimage d'un point est un ensemble fini. Si de plus n'a que deux valeurs critiques, 0 et 1 par exemple, l'image réciproque du segment réel [ 0, 1] R C trace un graphe connexe dans le plan. C'est un dessin au sens ci-dessus, dont les deux types de sommets correspondent aux préimages de 0 et 1.

c. Sur une surface compacte

Il est plus canonique de considérer qu'un dessin plan est dessiné sur la sphère C {} et non sur le plan. Le choix de la position sur la sphère est un marquage du dessin. C'est pour cela que nous avons défini un dessin plan comme dessin marqué de genre 0.

Si la surface n'est pas une sphère, mais une autre surface de Riemann compacte (de genre g) nous avons des dessins de genre g. C'est le cadre le plus général pour étudier la correspondance de Grothendieck.

II.1.2 Structures mathématiques

a. Combinatoire des graphes

La représentation visuelle d'un dessin est un graphe (non orienté), c'est-à-dire un ensemble de points qu'on relie par des traits. Nous définissons ceci plus rigoureusement :

On appelle multi-ensemble un ensemble fini dont les éléments peuvent être répétés plusieurs fois. Plus formellement, les multi-parties de cardinal k>0 sont des k-uplets, modulo une permutation, et les multi-parties non vides de S sont les éléments de MP*(S) = _k>0(S^k / _k).

On appelle hypergraphe un couple (S,A) où S est un ensemble fini de sommets et A est une multi-partie de MP*(S), les arêtes. Deux sommets membres d'une même arête sont reliés par celle-ci. Si un sommet apparaît plusieurs fois dans une même arête, on parle d'incidence multiple. Si une même arête apparaît plusieurs fois dans A, il s'agit d'une arête multiple. La valence d'une arête est son cardinal, la valence d'un sommet est le nombre de fois que celui-ci apparaît dans les arêtes de l'hypergraphe. On appelle graphe un hypergraphe dont les arêtes sont de valence 2. Une boucle est une arête dont les deux éléments sont le même sommet. On parle de graphe simple s'il n'y a ni boucles ni arêtes multiples : A est alors un ensemble de paires de S.

Un graphe ou un hypergraphe est connexe si tout couple de sommets est relié par un chemin, c'est-à-dire une suite d'arêtes ayant un sommet commun. Un graphe se représente visuellement par un ensemble de points (A), reliés par des traits (S). On parle de graphe planaire si celui-ci peut être dessiné dans le plan sans que deux arêtes se croisent. Dès qu'on considère le plongement (c'est-à-dire le tracé des sommets, reliés par des arêtes ne se croisant pas) d'un graphe dans une surface, on parle de graphe plan ou de carte.

Sur la figure II.1, ni le deuxième, ni le troisième graphe n'est plan, mais le deuxième est planaire. Le quatrième graphe n'est pas simple, le cinquième n'est pas connexe.

 
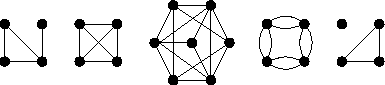
Figure II.1: Exemples de graphes.

b. Cartes d'une surface

Si nous dessinons un graphe sur une surface, cela nous donne un découpage de la surface suivant les arêtes du graphe. Si les morceaux ont tous la forme approximative d'un disque, on parle de carte cellulaire. Plus rigoureusement :

Soit X une surface (réelle) compacte et connexe orientable. Une cellule est un ouvert de X homéomorphe au disque ouvert (de R²). Un segment est un ouvert de X homéomorphe au segment ouvert (de R).

On appelle graphe cellulaire sur X ou carte un triplet (S, K, X) tel que S K X vérifient :

• S contient un nombre fini de points (les sommets du graphe)
• K - S est l'union disjointe d'un nombre fini de segments (les arêtes).
• X - K est l'union disjointe d'un nombre fini de cellules.

Deux sommets, arêtes ou cellules sont adjacents si l'un est dans l'adhérence de l'autre. Deux sommets ou deux faces sont adjacents s'ils sont adjacents à une même arête. Nous utiliserons le même terme, alors qu'on fait parfois la différence entre adjacence et incidence.

On définit le graphe sous-jacent comme suit : ses sommets sont les éléments de S, ses arêtes sont les paires de sommets adjacents. C'est un graphe connexe. Son graphe dual est celui-ci : ses sommets sont les cellules de la carte, ses arêtes sont les paires de cellules adjacentes.

On peut construire une carte duale en choisissant un point dans chaque cellule, ce qui donne l'ensemble fini S*. On trace un arc entre deux points correspondant à des cellules adjacentes, ce qui donne K* et une décomposition cellulaire S* K* X.

 
Figure II.2: Carte et carte duale (sur la sphère, et représentation plane).

Deux cartes sont homéomorphes s'il existe un homéomorphisme de X vers X' induisant des homéomorphismes de K vers K' et de S vers S'. Deux cartes isomorphes réalisent le même graphe.

Si les cellules sont des triangles (chaque cellule est adjacente à exactement trois sommets distincts, donc à trois arêtes) on dit que la carte est une triangulation.

Les cartes d'une surface sont des exemples très simples de CW-complexes finis.

c. Hypercartes

Sur une surface compacte connexe orientable X, on définit une hypercarte, ou hypergraphe cellulaire. C'est une carte où les cellules sont de trois types, que nous appelons hyper-sommets, hyper-arêtes et hyper-faces et où chaque sommet est adjacent à trois cellules, une de chaque type.

Les cellules adjacentes à une cellule donnée sont alors de deux types distincts, en alternance. Une cellule est donc délimitée par 2k arêtes, k est sa valence.

L'hypergraphe sous-jacent est défini comme suit : ses sommets sont les hyper-sommets, ses multi-arêtes sont les ensembles d'hyper-sommets ayant une hyper-arête adjacente en commun. L'hypercarte duale est celle où on échange le rôle des hyper-sommets et des hyper-faces.

 
Figure II.3: Hypercarte.

d. Combinatoire des groupes 

Lorsque nous définirons la monodromie, et pour toutes les allusions à la théorie de Galois, nous manipulons des groupes, la plupart du temps de cardinal fini ou opérant sur un emsemble. Il faut donc rappeler les définitions. À la fin de ce chapitre, nous utiliserons les notions plus compliquées de classes de conjugaison et de caractères irréductibles, nous profitons de ce paragraphe pour les définir et donner quelques propriétés.

Nous notons |G| le cardinal d'un groupe fini G, qu'on appelle ordre du groupe. Le centre d'un groupe est l'ensemble Z(G) des éléments qui commutent avec tout le groupe, c'est un sous-groupe.

Si H est un sous-groupe de G, nous notons H \ G = { gH | g élément de G } l'ensemble des translatés (classes à gauche ou cosets) de H. On dit que H est d'indice fini si cet ensemble est fini.

On définit deux sous-groupes : le normalisateur de H dans G, qui contient les éléments g de G tels que gH=Hg, et le centralisateur qui réunit les éléments de G commutant avec tous les éléments de H.

Deux éléments h et h' de G sont conjugués s'il existe g dans G tel que h' = g^-1 h g, ce qu'on écrit h' = h^g. C'est une relation d'équivalence entre les éléments de G, l'ensemble des classes de conjugaisons est noté Cl(G).

Rappelons qu'un groupe G opère sur un ensemble E s'il existe une action de G×E dans E telle que (gh). x = g.(h.x) et 1. x = x. Le stabilisateur d'un élément x de E est le sous-groupe H de G défini par H = { g élément de G | g . x = x }. L'orbite d'un élément x de E est l'ensemble { g . x } des images de x par le groupe. Un groupe agit transitivement si l'image par le groupe de tout élément de E est l'ensemble E en entier. Un groupe agit fidèlement si aucun élément non trivial de ce groupe n'agit trivialement sur E.

Le groupe Inn(G) des automorphismes intérieurs de G (qui sont h h^g) opère donc par conjugaison sur G. Pour tout sous-groupe H, le groupe G opère transitivement (par translation, g.(hH) = (gh)H ) sur les H \ G.

On appelle groupe de permutations un sous-groupe de _n. C'est donc un groupe opérant sur {1, ..., n}. La conjugaison dans un groupe de permutations correspond à une renumérotation de l'ensemble {1, ..., n}. Nous choisissons de noter les permutations par leur décomposition en cycles, en les faisant agir à droite. Ainsi le produit de (1,2) et de (2,3) est (1,2)(2,3)=(1,3,2).

Si G est un groupe, K un corps et V un espace vectoriel de dimension finie sur K, on appelle représentation linéaire une application : GGL(V) qui est un homomorphisme vers le groupe des automorphismes de V. Une représentation est irréductible s'il n'y a pas de sous-espace vectoriel propre de V qui soit stable par l'image de G. Toute représentation se décompose en somme directe de représentations irréductibles. On appelle caractère l'application de G dans K telle que   g Tr((g)) où Tr est la trace des endomorphismes linéaires. Un caractère irréductible est le caractère d'une représentation irréductible. On s'intéresse au cas où K = C. Les caractères sont constants sur chaque classe de conjugaison. Il y a autant de caractères irréductibles que de classes de conjugaisons. De même que nous avons noté Cl(G) l'ensemble de ses classes de conjugaison, nous notons X(G) l'ensemble des caractères irréductibles. Au paragraphe II.3.4.c. et pour tester la rigidité, nous aurons à calculer les valeurs des caractères irréductibles. Il suffit pour cela de regarder dans une table comme dans l'Atlas des groupes finis ([13], pour les groupes simples) ou d'utiliser un logiciel gratuit et efficace, tel GAP.

L'image de G par ses caractères irréductibles est dans un corps de nombres K. Cela nous permettra au paragraphe II.3.5.e. de parler de K-rationalité d'une classe de conjugaison. Nous appelons exposant du groupe fini G le plus petit commun multiple des ordres de ses éléments, que nous allons noter ici N, c'est un diviseur de l'ordre du groupe. L'image de G par X(G) est dans le corps cyclotomique Q(_N) où _N est une racine primitive N-ième de l'unité. Le groupe de Galois de Q(_N) sur Q est isomorphe au groupe (Z / NZ)^×. Il agit sur Cl(G) et sur X(G) comme suit : n élément de (Z / NZ)^× envoie c sur cⁿ, ensemble des puissances n-ièmes des éléments de c, et _n, élément de Gal( Q(_N) / Q) envoie élément de X(G) sur le caractère g (gⁿ). On note c* la réunion des cⁿ.

e. Variété analytique

L'autre aspect des dessins d'enfants se décrit à l'aide de revêtements. On parle ainsi de revêtement de surfaces de Riemann ou de revêtement de courbes algébriques. Nous allons donc définir une notion analytique de variété, différente de la notion de variété algébrique qu'on a vu au paragraphe I.1.4.b..

Une variété analytique (ou différentielle, ou topologique ; les variétés utilisées pour les dessins d'enfants peuvent être munies de toutes ces structures) de dimension m est un espace localement isomorphe à R^m, c'est-à-dire muni d'un atlas. Cela signifie qu'en tout point de la variété on peut définir une carte qui est ici un isomorphisme entre un voisinage de ce point et un ouvert de R^m, et que les cartes sont compatibles (analytiquement, différentiellement ou topologiquement) sur l'intersection des voisinages correspondants. Une variété est ainsi munie d'une topologie qui permet de considérer sa connexité et sa compacité. Elle est orientable si les cartes peuvent être orientées de façon compatible.

Si nous choisissons deux points b et c quelconques dans une variété X, un chemin de b à c est une application continue l de [0,1] dans X tel que l(0)=b et l(1)=c. Deux chemins l₀ et l₁ sont homotopes s'il existe de [0, 1] × [0, 1] dans X, continue et telle que (·, 0) = l₀(·), (·, 1) = l₁(·) et pour tout x, (0, x) = b et (1, x) = c. C'est une déformation continue de chemins. Un chemin de b à b est appelé lacet de point base b.

Les classes d'équivalence de lacets homotopes sur une variété connexe sont naturellement munies d'une structure de groupe, c'est le groupe fondamental de la variété, qu'on note ₁. Si tous les lacets d'une variété sont homotopes, elle est simplement connexe.

On peut remarquer que le groupe fondamental de la sphère S moins n points est le groupe libre engendré par n-1 boucles autour de tous ces points sauf un (la boucle autour du dernier point ôté est la composition des autres). Les classes d'homotopie de lacets correspondent en effet au nombre de tours autour des trous.

 
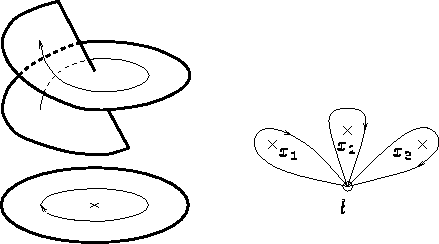
Figure II.4: Relèvement d'un lacet autour d'une valeur de ramification.
Générateurs du ₁ de S - {x₁, x₂, x₃}.

f. Revêtement

Soient deux variétés X et Y. Un revêtement (analytique, différentiel, ou topologique) est une application surjective de Y dans X, telle tout point de X admette un voisinage V dont la préimage est isomorphe à F × V où F est un ensemble discret. On appelle fibre la préimage d'un point. Le cardinal de F est constant sur chaque composante connexe de X. Si X est connexe, c'est le degré du revêtement. Un revêtement fini est un revêtement de degré fini.

Le revêtement universel d'une variété connexe est un revêtement connexe et simplement connexe, qui est unique à isomorphisme près.

Une surface est une variété analytique de dimension 2. Les courbes projectives lisses définies sur C peuvent être munies d'une structure de surface orientable. En particulier, P₁C est une sphère. Un morphisme de courbes algébriques irréductibles : YX est aussi appelé revêtement algébrique. C'est un revêtement ramifié de surfaces, ce qui siginifie qu'il existe un sous-ensemble discret R de X tel que la restriction de à ^-1(X - R) est un revêtement analytique. Les points de R sont appelés valeurs de ramification ou valeurs critiques et ^-1(R) est l'ensemble des points de ramification.

g. Relèvement et monodromie

Si nous avons un revêtement (non ramifié) : YX et un chemin l de b à c dans X et si on choisit un point de la fibre au dessus de b, on appelle relèvement l'unique chemin de Y partant de ce point et ayant pour image l par . Le point final du relèvement de l est donc dans la fibre au dessus de c.

Le théorème de monodromie affirme que ce point ne dépend que de la classe d'homotopie de l. Cela signifie que les relèvements de deux chemins homotopes aboutissent au même point.

le groupe fondamental de X agit donc en permutant la fibre du point base. Le groupe de permutations ainsi engendré est appelé monodromie. Il est transitif si, et seulement si, Y est connexe.

h. La sphère et la droite projective

Les dessins d'enfants peuvent être vus comme des revêtements de la sphère P₁C. Nous allons étudier un peu plus en détail les propriétés de la droite projective.

Par définition, les éléments de P₁K sont les droites de K² passant par l'origine (cf. § I.1.4.a.). Ce sont donc les couples (x : y) où (kx : ky)=(x : y) pour k élément de K^×. Pour tout corps, P₁K contient au moins les trois points (0 : 1), (1 : 1) et (1 : 0).

Les endomorphismes de P₁K sont les homographies (x : y) (ax + b : cx + d). où ad - bc est non nul. Les homographies sont en bijection avec les triplets de points distincts de P₁K, par exemple les images de (0 : 1), (1 : 1) et (1 : 0) par l'homographie.

Si nous identifions P₁K à K {} , avec (x : y) x / y si y est non nul et (x : 0) , les trois points précédemment cités sont 0, 1 et . Une homographie est alors l'application x (ax + b) / (cx + d). Lorsqu'on fixe , ce sont les similitudes directes x ax + b.

Il existe six homographies particulières, qui correspondent aux permutations de l'ensemble {0, 1, }. Ce sont x, 1/(1-x), (x-1)/x, x/(x-1), 1/x et 1-x.