Previous Up Next

2.2  The Heater

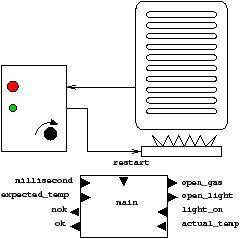
Consider the problem of a system which control a gas heater as informally depicted in figure 2.1.

 
Figure 2.1: The heater

The heater front has a green light indicating a normal functioning whereas the red light is turned on when some problem has occurred (security stop). In that case, the heater is stopped and it can be restarted by pushing a restart button. Moreover, a rotating button allows the user to indicate the expected temperature of the water.

The controller has thus the following inputs.

The outputs of the controller are the following:

The purpose of the controller is to keep the water temperature close to the expected temperature. Moreover, when this temperature must be heated, the controller turns on the gas and light for at most 500 millisecond. When the light is on, only the gas valve is maintained open. If there is no light after 500 millisecond, it stops for 100 millisecond and start again. If after three tests, there is still no light, the heater is blocked on a security stop. Only pushing the restart button allows to start again the process.

We start with the definition of a few scalar constants and two auxiliary functions.

let static low = 4
let static high = 4

let static delay_on = 500 (* in miliseconds *)
let static delay_off = 100

(* [count d t] returns [true] when [d] occurrences of [t] has been received *)
let node count d t = ok where
  rec ok = cpt = 0
  and cpt = d -> if t & not (pre ok) then pre cpt - 1 else pre cpt

let node edge x = false -> not (pre x) & x

The following node decides weather the heater must be turn on. We introduce an hysteresis mechanism to avoid oscillation. low and high are two threshold. The first version is a purely data-flow one whereas the second one (which is equivalent) uses the automaton construction.

(* controling the heat *)
(* returns [true] when [expected_temp] does not agree with [actual_temp] *)
let node heat expected_temp actual_temp = ok where
  rec ok = if actual_temp <= expected_temp - low then true
           else if actual_temp >= expected_temp + high then false
           else false -> pre ok

(* the same function using two modes *)
let node heat expected_temp actual_temp = ok where
  rec automaton
        False -> 
          do ok = false 
          unless (actual_temp <= expected_temp - low) then True
      | True ->
          do ok = true 
          unless (actual_temp >= expected_temp + high) then False
      end

Now, we define a node which turns on the light and gas for 500 millisecond then turn them off for 100 millisecond and restarts.

(* a cyclic two mode automaton with an internal timer *)
(* [open_light = true] and [open_gas = true] for [delay_on millisecond] *)
(* then [open_light = false] and [open_gas = false] for *)
(* [delay_off millisecond] *)
let node command millisecond = (open_light, open_gas) where
  rec automaton
        Open ->
          do open_light = true
          and open_gas = true
          until (count delay_on millisecond) then Silent
      | Silent ->
          do open_light = false
          and open_gas = false
          until (count delay_off millisecond) then Open
      end

The program which control the aperture of the light and gas is written below:

(* the main command which control the opening of the light and gas *)
let node light millisecond on_heat on_light = (open_light, open_gas, nok) where
  rec automaton
        Light_off ->
          do nok = false
          and open_light = false
          and open_gas = false
          until on_heat then Try
      | Light_on ->
          do nok = false
          and open_light = false
          and open_gas = true
          until (not on_heat) then Light_off
      | Try ->
          do
            (open_light, open_gas) = command millisecond
          until light_on then Light_on
          until (count 3 (edge (not open_light))) then Failure
      | Failure ->
          do nok = true 
          and open_light = false
          and open_gas = false
          done
      end

Finally, the main function connects the two parts.

(* the main function *)
let node main millisecond restart expected_temp actual_temp on_light =
                                       (open_light, open_gas, ok, nok) where
  rec reset
        on_heat = heat expected_temp actual_temp
      and
        (open_light, open_gas,nok) = light milisecond on_heat on_light
      and
        ok = not nok       
      every restart

Supposing that the program is written in a file heater.ls, the program can be compiled by typing:

% lucyc -s main heater.ls

which produces files heater.ml and main.ml, the later containing the transition function for the node main.

Previous Up Next