IV.5 Les groupes de Mathieu

IV.5.1 Contexte

Les propriétés axiomatiques définissant un groupe fini sont élémentaires et pourtant la classification des objets vérifiant ces propriétés est vraisemblablement le théorème le plus touffu des mathématiques. On commence par considérer les sous-groupes distingués (ceux qui sont stables par conjugaison). Il reste à classifier les groupes sans sous-groupes distingués, qu'on appelle groupes simples. Ceux-ci sont les groupes cycliques d'ordre premier, les groupes alternés (de degré 5 ou plus), les groupes de Chevalley et groupes de Chevalley "twisted", le groupe de Tits et les 26 groupes sporadiques.

Les cinq groupes de Mathieu (M₁₁ , M₁₂ , M₂₂ , M₂₃ et M₂₄) sont des groupes sporadiques. On peut en trouver des définitions comme groupes de permutations dans [45] et [12].

IV.5.2 Dessin correspondant à Aut(M₂₂)  

J'ai calculé par ma méthode numérique le revêtement utilisé par Malle [29] pour réaliser Aut(M₂₂) comme groupe de Galois sur Q(T). Ce calcul a été un peu plus difficile que les précédents car il y a de nombreuses étapes pour construire ce dessin. Il faut choisir soigneusement la façon dont on rajoute des points pour ne pas déséquilibrer la géométrie des étapes intermédiaires. Voir figures IV.10, IV.11, IV.12 et IV.13. Le temps de calcul est négligeable, puisque le dessin final (marqué avec une face à l'infini) est défini sur Q(-11).

 
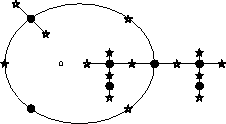
Figure IV.5: Aut(M₂₂) : aspect combinatoire du dessin.

On peut facilement vérifier sur la figure IV.5 que la monodromie ( , ₀ , ₁) du revêtement est dans les classes 11A, 4C et 2B et engendre bien le groupe Aut(M₂₂).
= (1,2,3,4,5,6,7,8,9,10,11)(12,13,14,15,16,17,18,19,20,21,22),
₀ = (1,9,3,2)(4,8,17,21)(5,20,19,6)(12,22,16,13)(7,18)(10,11)(14,15),
₁ = (3,8)(4,20)(6,18)(7,17)(9,11)(13,15)(16,21)(1)(2)(5)(10)(12)(14)(19)(22).

IV.5.3 Dessins correspondant à M₂₄

``The group M₂₄ is one of the most remarkable of all finite groups'' [13], en particulier parce qu'il intervient dans la structure des autres groupes sporadiques. On s'intéresse donc au calcul de dessins dont la monodromie engendre M₂₄.

 
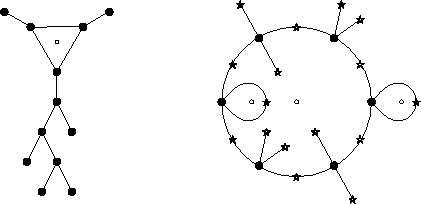
Figure IV.6: M₂₄ : extraterrestre et dessin de Conder.

Le premier dessin (propre) de la figure IV.6, que Zvonkine a appelé extraterrestre, définit une extension de Q(T)(-7) de groupe de Galois M₂₄. La monodromie est :
= (1,2,3)(4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24),
₀ = (1,7,5)(2,4,23)(3,22,8)(9,21,19)(10,18,12)(13,17,15),
₁ = (1,4)(2,22)(3,7)(5,6)(8,21)(9,18)(10,11)(12,17)(13,14)(15,16)(19,20)(23,24).

Conder [12] donne une définition de M₂₄ qui correspond à un revêtement de genre 0 défini sur le corps de degré 5 de discriminant -2³11³23 et de polynôme générateur X⁵ - X⁴ - X² - 4X + 4. Le dessin correspondant est le second de la figure IV.6.

IV.5.4 Revêtement correspondant à M₂₄  

a. Rationalité

Matzat [33] a prouvé, à partir de calcul dus à F. Häfner, qu'il existe une extension régulière de Q(T) de groupe de Galois M₂₄, ramifiée au dessus de quatre points. Il n'avait pas réussi à le calculer explicitement, ce que nous avons mené à bien (voir l'article [23]).

La preuve de l'existence d'un modèle rationnel de ce revêtement est compliquée, elle permet de savoir que le calcul explicite du revêtement peut effectivement aboutir à un modèle rationnel, mais elle n'est pas nécessaire pour mener ces calculs à terme.

Comme le revêtement correspondant à cette extension de Q(T) n'a pas de célibataire, nous obtiendrons d'abord un modèle sur Q(i). Nous en déduisons ensuite un modèle sur Q, le polynôme P ci-dessous, à coefficients dans Q(T) :

P(u) = (1+u²) B(u)² + (T - A(u))²

avec A(u) = 115641803437317009004628044535281448962593335543045088145221615616u¹² + 626355604609903799744911431879812361696225381618360944350772330496u¹¹ + 857783185877096409511863319468234125688211122856849368609978318848u¹⁰ + 88080740861115132546504599272290397834597343353226396588729958400u⁹ - 2044360579432951434692976374444394700879262571672409913586424315904u⁸ - 5475143722890558821885980641854499068186361905255250703867300741120u⁷ - 7915098194760821823142546569353472116219954897777155569247687385088u⁶ - 8606261485891070160857017864300195449330895913416748672060967716864u⁵ - 6892242684910426245304385038953482144305957644307673212590062039792u⁴ - 4211432359386694117643177642371531969039977445473402080794314842304u³ - 1872082062997662285544516575637661132224190147802824412182076667540u² - 535658851956460224909548877202498831723299104598077260690473552648u - 10539752687297944130116169432500844400960251281699137159101902851925/108
et
B(u) = 497930855073541362607491227688032103381849370443591345788311044096u¹⁰ + 2247466124279729012772791671105119975141086793312284796250730004480u⁹ + 4511506352550421307509247841822653344621269494040738994345402695680u⁸ + 6412425694206308627270788749164116952920226584905116935357763420160u⁷ + 6416753127617241617644191979736728938801492606944566101914795376640u⁶ + 4464975149990471124875637674124629993019905811395113462955040856064u⁵ + 2003277439178423819468870064822584402702435670423637216226474276864u⁴ + 138777346101247571424430364531859413923341606824997843710647542784u³ - 380956273497114446731514632739210828177910748030971539812432183456u² - 281510287298644718070258765258190530609884596662730222193000312096u - 65579751162139732289229065103774858338759236102619183144664480716.

b. Éclatement de la singularité

Nous connaissons la monodromie (_a, _b, _c, _d) du revêtement. Nous en déduisons la monodromie (_a, _t= _{b c}, _d) d'un revêtement dégénéré, où les valeurs de ramification correspondant à b et c sont confondues.

 
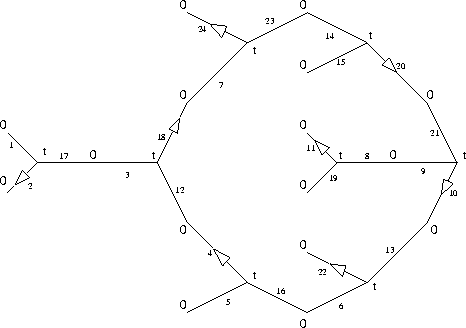
Figure IV.7: M₂₄ : ^-1([0, t]) pour un revêtement dégénéré, avec flèches indiquant la direction d'éclatement des singularités

Lorsque nous ``éclatons'' la singularité en t, chaque point au dessus de la valeur de ramification t se sépare en plusieurs points de ramification au dessus de b ou c. Leur nombre dépend de leurs valences, et la direction de l'iclatement est une conséquence de la façon dont sont mélangées les orbites des permutations _b et _c.

 
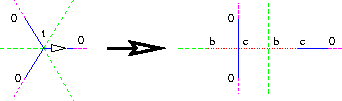
Figure IV.8: Éclatement des singularités.

c. Calcul de nombreuses solutions

Le paramètre (non rationnel) de la famille de Hurwitz le plus simple à manipuler est la position relative des quatre valeurs de ramification. Nous pourrions utiliser le birapport de ces valeurs, mais il est encore plus simple, et pas moins efficace, de fixer une de ces valeur à et de bouger (presque) indifféremment les trois autres.

Sachant que 144 (c'est ici la valeur de l ⁱ_C) revêtements correspondent à chaque position des valeurs de ramification, nous faisons agir (progressivement) le groupe de tresses à quatre brins pour obtenir la description de tous ces revêtements. En pratique, nous fixons un des trois points mobile, nous faisons tourner les deux autres l'un autour de l'autre, puis nous changeons de point fixé.

d. Recherche d'un paramètre de la famille de revêtements  

La méthode décrite au paragraphe I.3.4.e. permet de trouver un paramètre rationnel d'une courbe. Mais, dans le cas qui nous intéresse, lorsque nous avons fixé 0 0, la variété solution du système est de dimension 2. L'un des degrés de liberté correspond au paramètre de la famille de Hurwitz, l'autre à l'échelle du dessin.

Pour trouver le paramètre qui nous intéresse, nous supprimons l'influence du paramètre d'échelle en ne considérant que des fonctions des variables du système qui soient invariantes par changement d'échelle.

Nous avons construit une fonction _P et une fonction _Q, fonctions symétriques des variables correspondant aux points de ramification d'ordre 2 (pour _P) ou 1 (pour _Q). Une relation polynomiale de degré 4 définit la courbe où vit le couple (_P , _Q). Nous trouvons un paramètre de cette courbe.

Ensuite, nous avons choisi une fonction _P qui rompt la symétrie de la construction de _P. Nous trouvons une relation polynomiale entre et _P qui, après désingularisation, donne un paramètre t. C'est un paramètre rationnel du revêtement.

Il suffit donc de donner une valeur rationnelle à t et de calculer le revêtement correspondant pour avoir un point rationnel de la famille, et donc une extension de Q(T).

 
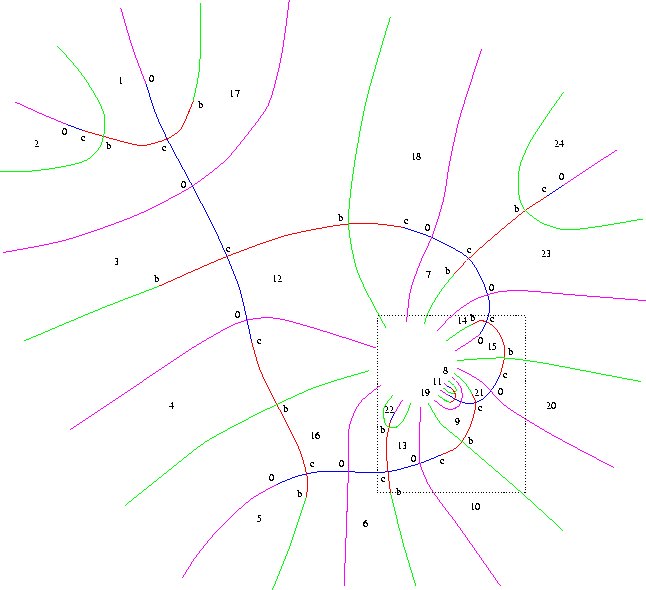
Figure IV.9: M₂₄ : le revêtement final

 
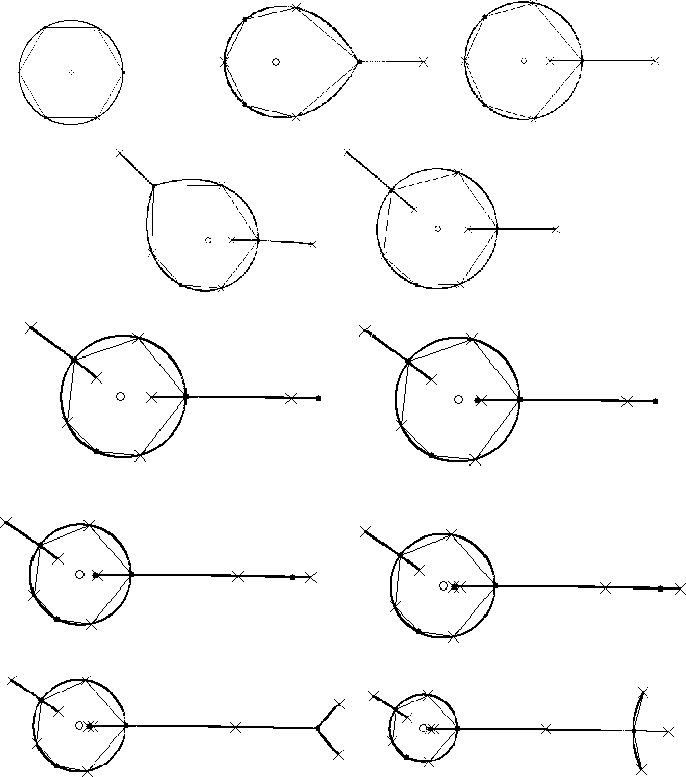
Figure IV.10: Aut(M₂₂) : onze premières étapes.

 
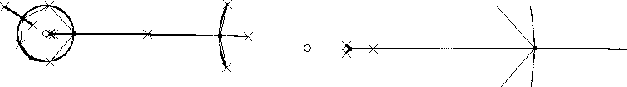
Figure IV.11: Aut(M₂₂) : douzième étape avec angrandissement du centre.

 
Figure IV.12: Aut(M₂₂) : treizième à seizième étapes.

 
Figure IV.13: Aut(M₂₂) : dessin final.