III. Calcul de la fonction de Belyi
La correspondance de Grothendieck pose (entre autres) le problème
de son calcul explicite. Étant donnée une paire de Belyi
(X,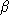 )
Leila Schneps [37, p60] propose,
dans le cas d'un dessin propre de genre 0,
une méthode rigoureuse
*
pour calculer la monodromie
(
)
Leila Schneps [37, p60] propose,
dans le cas d'un dessin propre de genre 0,
une méthode rigoureuse
*
pour calculer la monodromie
( 0,
0,
 1,
1,

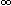 )
et la préimage de [0,1] par
)
et la préimage de [0,1] par
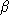 .
Cette méthode s'applique facilement au cas des dessins non nécessairement
propres.
Pour le problème inverse, la méthode employée est souvent
la résolution d'un système algébrique dont les inconnues
sont les paramètres de la fonction de Belyi.
Nous commencerons par présenter la construction d'un tel
système. Nous énumérerons ensuite quelques autres
méthodes de calcul d'une fonction de Belyi.
Nous concluons en donnant des résultats géométriques
d'approximation, qui permettent d'aider le calcul
en s'inspirant d'une intuition géométrique.
.
Cette méthode s'applique facilement au cas des dessins non nécessairement
propres.
Pour le problème inverse, la méthode employée est souvent
la résolution d'un système algébrique dont les inconnues
sont les paramètres de la fonction de Belyi.
Nous commencerons par présenter la construction d'un tel
système. Nous énumérerons ensuite quelques autres
méthodes de calcul d'une fonction de Belyi.
Nous concluons en donnant des résultats géométriques
d'approximation, qui permettent d'aider le calcul
en s'inspirant d'une intuition géométrique.
- III.1 Le système algébrique
- III.1.1 Paramètres de la paire de Belyi
- a. Présentation du problème
b. Représentation du problème
c. En genre 0
- III.1.2 Les dessins de genre 0
- a. Les données du système
b. Aspect de l'application de Belyi
c. Cas où l'infini n'est pas ramifié
d. Placement d'un célibataire à l'infini
- III.1.3 Cas des arbres.
- a. Polynômes de Shabat
b. Recherche numérique des racines
- III.2 Autres méthodes
- III.2.1 Méthodes directes
- a. La projection d'une courbe elliptique sur la première coordonnée
b. Construction de Belyi
- III.2.2 Séries de Puiseux
- III.3 Approximation de dessins
- III.3.1 Résolution par étapes dans C
- a. Idée générale
b. Suppression d'un sommet de valence 1
c. Ajout d'un sommet de valence 1
- III.3.2 Résolution approchée dans Qp
- III.3.3 Approximation de revêtements ramifiés au dessus de 4 points
- a. Pour le calcul d'un tel revêtement
b. Pour le calcul d'un dessin
) Leila Schneps [37, p60] propose, dans le cas d'un dessin propre de genre 0, une méthode rigoureuse * pour calculer la monodromie (
0,
1,
) et la préimage de [0,1] par
. Cette méthode s'applique facilement au cas des dessins non nécessairement propres. Pour le problème inverse, la méthode employée est souvent la résolution d'un système algébrique dont les inconnues sont les paramètres de la fonction de Belyi. Nous commencerons par présenter la construction d'un tel système. Nous énumérerons ensuite quelques autres méthodes de calcul d'une fonction de Belyi. Nous concluons en donnant des résultats géométriques d'approximation, qui permettent d'aider le calcul en s'inspirant d'une intuition géométrique.