Project-Trec: Point Processes, Stochastic Geometry and Random Geometric Graphs

Inria / Raweb 2010
Presentation of the Project Trec

Section: New Results

Point Processes, Stochastic Geometry and Random Geometric Graphs

Participants : François Baccelli, Bartłomiej Błaszczyszyn, Pierre Brémaud, Yogeshwaran Dhandapani, Mir Omid Haji Mirsadeghi, Justin Salez.

Stochastic Comparison of Random Measures and Point Processes

Stochastic geometric models (in particular these of wireless networks) are in general investigated in Poisson point process setting. Due to the difficulty (or even impossibility) of obtaining closed-form expressions for characteristics of these models in non-Poisson settings, we attempt a qualitative study of these characteristics, in particular by comparison to Poisson setting. Directionally convex ordering of point processes proved to be particularly pertinent in regard to this matter, as shown in [61] . This year we have continued working with this order, in particular using it to compare the clustering and percolation properties of point processes; cf. Section 6.4.2 . The whole research axis was being developed in the PhD thesis [6] of D. Yogeshwaran defended in 2010.

Percolation and Directionally Convex Ordering

Comparisons of Ripley's functions and pair correlation functions seem to indicate that point processes higher in directionally convex (dcx ) order cluster more. Simulation of various points processes comparable in this order, in particular in the class of the so called perturbed lattice point processes , also confirm this observation. These simulations, as well as some heuristics, indicate also that clustering of a point process negatively impacts the percolation of the related continuum percolation model, called also the Boolean model. We moved toward a formal statement of this heuristic. Namely, we defined two critical radii for percolation of the Boolean model called the lower and upper critical radii as these sandwich the usual critical radius for percolation of the Boolean model. We showed that dcx order preserves the upper critical radii and reverses the lower critical radii. Following this observation we considered a class of point processes, which we call sub-Poisson ; these are point processes that can be dominated in dcx by some Poisson point process. For this class, we extended the classical result on the existence of phase transition in the percolation of the Gilbert's graph (called also the Boolean model, and in the historical result generated by a homogeneous Poisson point process). We also extended a recent result of the same nature for the SINR graph, to sub-Poisson point processes. This work is a part of the PhD thesis [6] of D. Yogeshwaran defended in 2010. Partial results have been presented at the Allerton Conference in 2010; cf [28] , [48] . A more complete, journal paper [62] is under preparation.

Information Theory and Stochastic Geometry

In a joint work with V. Anantharam [UC Berkeley], [40] , we studied the Shannon regime for the random displacement of stationary point processes. Let each point of some initial stationary point process in n -dimensional Euclidean space give rise to one daughter point, the location of which is obtained by adding a random vector to the coordinates of the mother point, with all displacement vectors independently and identically distributed for all points. The decoding problem is then the following one: the whole mother point process is known as well as the coordinates of some daughter point; the displacements are only known through their law; can one find the mother of this daughter point? The Shannon regime is that where the dimension n tends to infinity and where the logarithm of the intensity of the point process is proportional to n . We showed that this problem exhibits a sharp threshold: if the sum of the proportionality factor and of the differential entropy rate of the noise is positive, then the probability of finding the right mother point tends to 0 with n for all point processes and decoding strategies. If this sum is negative, there exist mother point processes, for instance Poisson, and decoding strategies, for instance maximum likelihood, for which the probability of finding the right mother tends to 1 with n . We then used large deviations theory to show that in the latter case, if the entropy spectrum of the noise satisfies a large deviation principle, then the error probability goes exponentially fast to 0 with an exponent that is given in closed form in terms of the rate function of the noise entropy spectrum. This was done for two classes of mother point processes: Poisson and Matérn. The practical interest to information theory comes from the explicit connection that we also establish between this problem and the estimation of error exponents in Shannon's additive noise channel with power constraints on the codewords.

Random Geometric Graphs

Random Geometric Graphs (RGG) have played an important role in providing a framework for modeling in wireless communication, starting with the pioneering work on connectivity by Gilbert (1961); [68] . Vertices or points of the graphs represent communicating entities such as base stations. These vertices are assumed to be distributed in space randomly according to some point process, typically a Poisson point process. En edge between two points means that the communicating entities able to communicate with each other. In the classical model an edge exists between any two pair of nodes if the distance between them is less than some critical threshold. A variant of this classical model that exhibits the union of the coverage regions of all nodes is also referred to in stochastic geometry as the Boolean model. In the following, more fundamental works, we studied some variants and extensions of the classical models, more or less related to wireless communication networks.

AB Random Geometric Graphs

We investigated percolation in the AB Poisson-Boolean model in d -dimensional Euclidean space, and asymptotic properties of AB random geometric graphs on Poisson points in [0, 1]^d . The AB random geometric graph we studied is a generalization to the continuum of a bi-partite graph called the AB percolation model on discrete lattices. Such an extension is motivated by applications to secure communication networks and frequency division duplex networks. The AB Poisson Boolean model is defined as a bi-partite graph on two independent Poisson point processes of intensities $\lambda$ and $\mu$ in the d -dimensional Euclidean space in the same manner as the usual Boolean model with a radius r . We showed existence of AB percolation for all d $\ge$ 2 , and derived bounds for a critical intensity. Further, in d = 2 , we characterize a critical intensity. The set-up for AB random geometric graphs is to construct a bi-partite graph on two independent Poisson point process of intensities n and cn in the unit cube. We provided almost sure asymptotic bounds for the connectivity threshold for all c>0 and a suitable choice of radius cut-off functions r_n(c) . Further for c<c₀ , we derived a weak law result for the largest nearest neighbor radius. This work is a part of the PhD thesis [6] of D. Yogeshwaran defended in 2010. It has also been submitted for the publication as a research article [50] .

Spatial percolation model for delay tolerant networks

Delay Tolerant Networks, in the simplest terms, are networks that take into account the time-delay at nodal points for the transmission of information in a network. First passage percolation models have been found to be useful for study of transmission of information along networks. We consider spatial growth models on stationary graphs constructed on point processes, similar in the spirit of continuum first passage percolation models. The dynamic governing this network model is the delayed propagation of the information at the vertices of the graph. Depending on the manner of the time-delay and information dissemination time, one can obtain various models. We are analyzing this class of models with the hope of obtaining shape theorem for the spread of information. These models combine the dynamics of both the first passage percolation models and Richardson growth models.

Optimal Paths on Space-Time SINR Graphs

In the context of the opportunistic routing described in Section 6.1.2.4 , in a more fundamental paper [53] we studied optimal paths in wireless networks in terms of first passage percolation on some space-time SINR graph. We establish both “positive” and “negative” results on the associated the percolation delay rate (delay per unit of Euclidean distance called in the classical terminology time constant). The latter determines the asymptotics of the minimum delay required by a packet to progress from a source node to a destination node when the Euclidean distance between the two tends to infinity. The main negative result states that the percolation delay rate is infinite on the random graph associated with a Poisson point process under natural assumptions on the wireless channels. The main positive result states that when adding a periodic node infrastructure of arbitrarily small intensity to the Poisson point process, the percolation delay rate is positive and finite.

Finding optimal space-time paths studied above needs the knowledge of the future which is impossible in practice. So an interesting question consists in looking for local (both in time and space) algorithms. In [53] we proved the convergence of the radial routing under the SINR setup. Another work in progress consists in analyzing the directional algorithm. In this algorithm packet uses the best link in the desired direction as the next node.

Ergodicity of a Stress-Release-Point-Process Seismic Model with Aftershocks

The times of occurrence of earthquakes in a given area of seismic activity form a simple point process N on the real line, where N((a, b]) is the number of shocks in the time interval (a, b] . The dynamics governing the process can be expressed by the stochastic intensity $\lambda$ (t) . In the stress release model, for t $\ge$ 0 , $Im4 ${\#955 {(t)}=e^{X_0+ct-\#8721 _{n=1}^{N((0,t])}Z_n}}$$ , where c>0 and 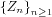$Im5 ${{Z_n}}_{n\#8805 1}$$ is an i.i.d. sequence of non-negative random variables with finite expectation, whereas X₀ is some real random variable. The process $Im6 ${X{(t)}=X_0+ct-\#8721 _{n=1}^{N((0,t])}Z_n}$$ is known to be ergodic.

Another model of interest in seismology is the Hawkes branching process, where the stochastic intensity is $Im7 ${\#955 {(t)}=\#957 {(t)}+\#8747 _{(0,t]}h{(t-s)}N{(ds)}}$$ , where h is a non-negative function, called the fertility rate and $\nu$ is a non-negative integrable function. Such point process appears in the specialized literature under the name ETAS (Epidemic Type After-Shock and is used to model the aftershocks. 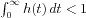It is well known that the corresponding process “dies out” in finite time under the condition $Im8 ${\#8747 _0^\#8734 h{(t)}~dt\lt 1}$$ .

A model mixing stress release and Hawkes aftershocks is

$Im9 ${\#955 {(t)}=e^{X_0+ct-\#8721 _{n=1}^{N((0,t])}Z_n}+Y_0e^{-\#945 t}+k\#8747 _{(0,t]}e^{-\#945 (t-s)}~N{(ds)},}$$

where $\alpha$ >0 . The positive constant c is the rate at which the strain builds up. If there is a shock at time t , then the strain is relieved by the quantity Z_N(t) . Each shock (primary or secondary) at time t generates aftershocks according to a Poisson process of intensity 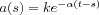$Im10 ${a{(s)}=ke^{-\#945 (t-s)}}$$ . In [10] , we gave necessary and sufficient conditions of ergodicity for this model.

Logo Inria