Signal representations for image classification need to be invariant with respect to the transformations which do not affect our ability to recognize. An important instance of these transformations is due to physical transformations, such as translations, dilations or rotations. Besides invariance, signal representations also need to be continuous with respect to signal deformations, and should capture enough signal information so that they can discriminate between different signal classes.

Scattering transforms build invariant, stable and informative representations through a non-linear, unitary transform, which delocalizes signal information into scattering decomposition paths. They are computed with a cascade of wavelet modulus operators, and correspond to a convolutional network where filter coefficients are given by a wavelet operator.

Thanks to their invariance and stability properties, scattering operators linearize deformations. This linearization property can be exploited to build linear generative classifiers in the scattering domain, which are computed with simple class-conditional PCA. When applied to stationary textures, scattering transforms provide new texture descriptors, incorporating high order moments which can discriminate non-Gaussian properties. As a result, state-of-the-art classification results are obtained on hand-written digit recognition and texture classification.

The Scattering transform shares some properties with the Fourier modulus transform. It has good frequency localization, it is translation invariant and it is unitary:

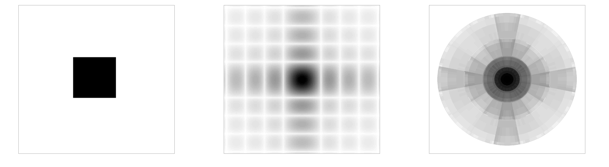
f = indicator of a square

Modulus of the Fourier transform of f

Scattering transform of f

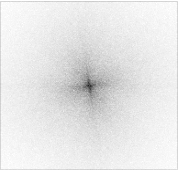
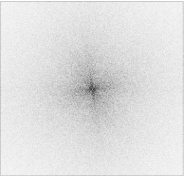
However, the Scattering transform is also stable with respect to small deformations. In this example, a Gabor atom is slightly deformed with a dilation and a rotation. Most of the Fourier energy is displaced to other frequencies, whereas most of the scattering energy remains stable:

f = Gabor atom of varying frequency and direction

Modulus of the Fourier transform of f

Scattering transform of f

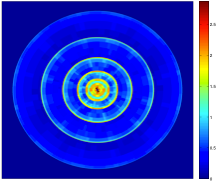
Besides, scattering coefficients capture high-order moments of stationary processes, as opposed to the Fourier power spectrum:

X1, X2 = Two realizations of stationary textures. X2 is obtained by equalizing random white noise according to the spectrum of X1.	Power spectrum of X1, X2.	Scattering transform of X1, X2. High order scattering coefficients discriminate between the Gaussian process X2 and the non-gaussian X1.

Classification Results

MNIST Digit

MNIST Digit database consists in 60.000 training images of digits and 10.000 training. The following results are reported in the paper , , .

Training Size	Raw Pixels		Windowed Fourier		Scatt \( m_\max = 1\)		Scatt \( m_\max = 2\)		Conv. Net.
	PCA	SVM	PCA	SVM	PCA	SVM	PCA	SVM
300	14.5	15.4	7.35	7.4	5.7	8	\( \bf{4.7} \)	5.6	7.18
1000	7.2	8.2	3.74	3.74	2.35	4	\( \bf{2.3} \)	2.6	3.21
2000	5.8	6.5	2.99	2.9	1.7	2.6	\( \bf{1.3} \)	1.8	2.53
5000	4.9	4	2.34	2.2	1.6	1.6	\( \bf{1.03} \)	1.4	1.52
10000	4.55	3.11	2.24	1.65	1.5	1.23	0.88	1	\( \bf{0.85} \)
20000	4.25	2.2	1.92	1.15	1.4	0.96	0.79	\(\bf{0.58}\)	0.76
40000	4.1	1.7	1.85	0.9	1.36	0.75	0.74	\( \bf{0.53} \)	0.65
60000	4.3	1.4	1.80	0.8	1.34	0.62	0.7	\( \bf{0.43} \)	0.53

CUReT

CUReT is a standard database of texture images. The following results are reported in the paper , ,

Training Size	Raw Pixels	Fourier Spectrum	Scat. \(m_{\max}=1\)	Scat. \(m_{\max}=2\)	Textons	MRF
	PCA	PCA	PCA	PCA
46	17	1	0.5	\( \bf{0.2} \)	1.53	2.4

OUTex 10

OUTex TC10 is a texture database with no rotation in the training set but all possible rotation in the testing set and thus requires built-in rotation invariant. The following results are reported in the paper Combined Scattering for Rotation Invariant Texture Analysis, Sifre L. and Mallat S., Proceedings of the ESANN 2012 conference, Apr. 2012. (PDF)

Training set	\( \text{LBP}^{riu2} + \) \( \text{VAR}_{(8,1) + (16,2) + (24,3)} \)	LBP-HF	RI-LPQ	Combined scattering \( m_{\max} = 1 \) \( \widetilde{m}_{\max}=2 \)	Combined scattering \( m_{\max}= 2 \) \( \widetilde{m}_{\max}=0 \)	Combined scattering \( m_{\max}= 2 \) \( \widetilde{m}_{\max}=1 \)	Combined scattering \( m_{\max}= 2 \) \( \widetilde{m}_{\max}=2 \)
rotation	97.7	96.59	98.26	96.72	97.73	98.62	\(\textbf{98.75} \)
rotation + tilt	NC	67.50	78.02	81.61	89.38	92.89	\(\textbf{93.07}\)