Anisotropic Laplace-Beltrami Operators for Shape Analysis
In Sixth Workshop on Non-Rigid Shape Analysis and Deformable Image Alignment (NORDIA), 2014
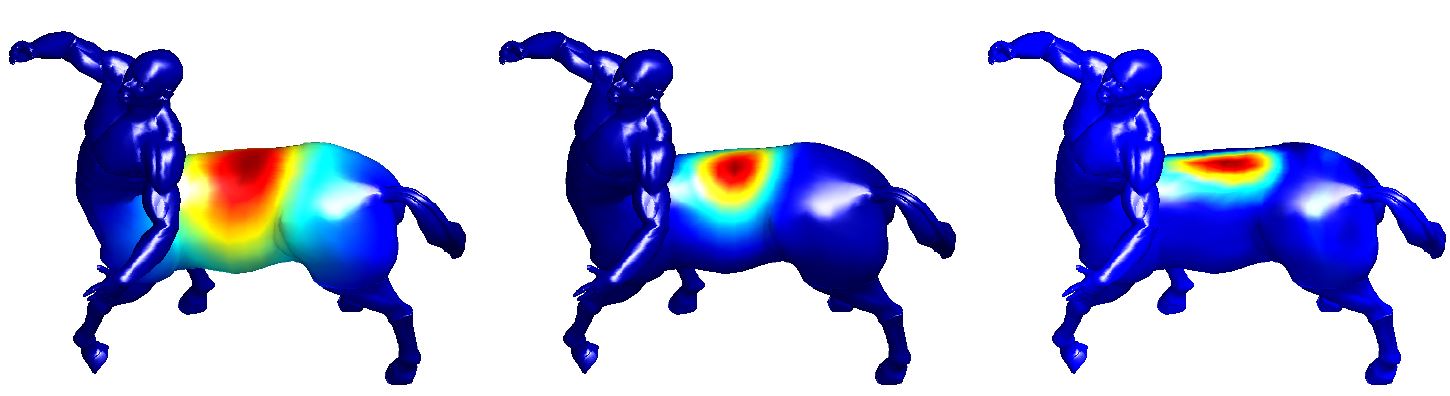
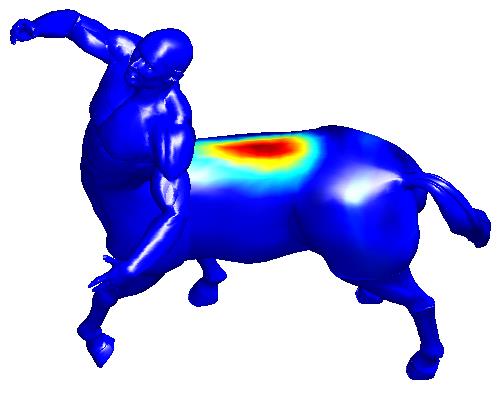
Anisotropic Laplace-Beltrami Operators for Shape Analysis
In Sixth Workshop on Non-Rigid Shape Analysis and Deformable Image Alignment (NORDIA), 2014
The documents contained in these directories are included by the contributing authors as a means to ensure timely dissemination of scholarly and technical work on a non-commercial basis. Copyright and all rights therein are maintained by the authors or by other copyright holders, notwithstanding that they have offered their works here electronically. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright.