Exercice 1 - Élections régionales
Le fichier Elections.txt contient le résultat du premier tour des élections régionales du 14 mars 2010 à Paris. Les résultats sont regroupés arrondissement par arrondissement (une ligne vide est utilisée pour les séparer) et affiche sur une ligne le nom du candidat et sur la ligne suivante le nombre de votes obtenus.
Écrire un script Python chargeant le fichier dans un array à deux dimensions associant aux candidats et aux arrondissement le nombre de votes obtenus.
-
Modifier le script pour qu'il calcule le résultat de l'élection à Paris.
- Modifier le script pour qu'il fournisse une estimation des résultat du second tour à Paris en créant une matrice correspondant aux reports de votes probables.
-
Modifier le script pour qu'il calcule le coefficient de corrélation des votes correspondant à deux arrondissements quelconques puis qu'il affiche les arrondissements où les votes sont les plus corrélés.
- Modifier le script pour qu'il affiche sous forme d'un diagramme circulaire (dit "en camembert") les résultats cumulés d'une liste d'arrondissements entrée par l'utilisateur.
from scipy import *
from pylab import *
resultats = open('Elections.txt','r')
res = resultats.readlines()
listenoms = []
for i in range(12):
listenoms = listenoms+[res[2*i]]
votes = zeros([12,20], dtype = int)
for i in range(12):
for j in range(20):
votes[i,j]=int(res[2*i+1+25*j])
# On veut le nombre de votes du
# candidat i dans l'arrondissement j
print "--------------------------"
print "| Resultats premier tour |"
print "--------------------------"
for i in range(12):
print listenoms[i],
print (float(votes[i].sum()*100))/(votes.sum())
reportdevoix = zeros([12,12])
reportdevoix[0,0]=0.9 # Report UMP
reportdevoix[8,8]=0.9 # Report PS
reportdevoix[8,1]=0.8 # Report LO
reportdevoix[0,2]=0.8 # Report FN
reportdevoix[8,3]=0.8 # Report EC
reportdevoix[8,6]=0.8 # Report FG
reportdevoix[0,7]=0.8 # Report LC
reportdevoix[0,9]=0.8 # Report DVD
reportdevoix[8,10]=0.8 # Report NPA
votes2=dot(reportdevoix,votes)
print "---------------------------"
print "| Resultats deuxieme tour |"
print "---------------------------"
for i in [0,8]:
print listenoms[i],
print (float(votes2[i].sum()*100))/(votes2.sum())
# Pour la suite : utiliser corrcoef
# prend en entree une matrice de donnees
# retourne une matrice ou la case (i,j) contient
# la valeur du coefficient de correlation entre la ieme ligne
# et la jieme ligne
votespararrondissement = votes.T
print "-------------------------"
print "| Correlation des votes |"
print "-------------------------"
print "Votes les plus correles dans les arrondissements ",
val = (corrcoef(votespararrondissement)-eye(20)).max()
for i in range(20):
for j in range(i,20):
if corrcoef(votespararrondissement)[i,j]==val:
print i+1, " et ", j+1
# Diagramme circulaire dans le 1er arrondissement
pie(votes.T[0],explode = None,labels=listenoms,\
autopct='%1.1f%%',shadow=True)
show()
Exercice 2 - Ensemble de Mandelbrot
D'après Wikipédia
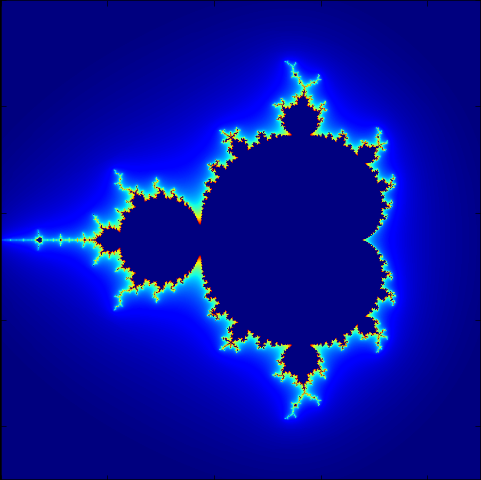
L'ensemble de Mandelbrot est une fractale qui est définie comme l'ensemble des points c du plan complexe pour lesquels la suite récurrente définie par : zn+1 = zn2 + c et la condition z0 = 0 ne tend pas vers l'infini (en module). Si nous reformulons cela sans utiliser les nombres complexes, en remplaçant zn par le couple (xn, yn) et c par le couple (a, b) alors nous obtenons: xn+1 = xn2 - yn2 + a et yn+1 = 2xnyn + b.
Il peut être démontré que dès que le module de zn est strictement plus grand que 2 (zn étant sous forme algébrique, quand xn2 + yn2 > 2), la suite diverge vers l'infini, et donc c est en dehors de l'ensemble de Mandelbrot. Cela nous permet d'arrêter le calcul pour les points ayant un module strictement supérieur à 2 et qui sont donc en dehors de l'ensemble de Mandelbrot. Pour les points de l'ensemble de Mandelbrot, i.e. les nombres complexes c pour lesquels zn ne tend pas vers l'infini, le calcul n'arrivera jamais à terme, donc il doit être arrêté après un certain nombre d'itérations déterminé par le programme.
Écrire un script qui affiche (une approximation de) l'ensemble de Mandelbrott.
from scipy import *
import pylab
def mandelbrot(h, w, maxit=15):
x = linspace(-3,1.5,w)
y = array(matrix(linspace(-1.5,1.5,h)).T)
c = x + y*1j
z = c.copy()
divtime = maxit + zeros((h, w), dtype=int)
restant = ones((h, w), dtype=bool) #
for i in range(maxit):
z[restant] = z[restant]*z[restant] + c[restant]
# Mise a jour des points restants
div = abs(z*restant) > 2
# Matrice booleene indiquant la divergence
divtime[div] = i
# Mise a jour du temps de divergence
restant &= ~div
# Mise a jour des points restants
z = z**2 + c # Lissage pour une figure plus jolie
z = z**2 + c
divtime = divtime + 2 - log(log(abs(z) + 1))/log(2)
return divtime
M = (mandelbrot(900, 1350, 30)/30*768).astype(int)
M[(M >= 768) | (M < 0)] = 0
pylab.imshow(M)
pylab.show()