 |  |


The language is a functional language, with a syntax close to Objective Caml. As in Lustre, every ground type or any scalar value imported from the host language, Objective Caml, is implicitly lifted to streams. Thus:
int stands for the type of streams of integers,
1 stands for the constant stream of values 1,
+ adds point-wisely its two input streams. It can be seen
as an adder circuit, in the same way, & can be seen as an
“and” gate.Program executions can be represented as chronograms, showing the sequence of values taken by streams during the execution. The example below shows five streams, one per line. The first line shows the value of a stream c, which has the value t (true) at the first instant, f (false) at the second one, and t at the third. The notation …indicates that the stream has more values (it is infinite), not represented here. Similarly, the following lines define x and y. The fourth line define a stream obtained by adding x and y, addition is done point-wisely.
| c | t | f | t | … |
| x | x0 | x1 | x2 | … |
| y | y0 | y1 | y2 | … |
| x+y | x0+y0 | x1+y1 | x2+y2 | … |
| if c then x else y | x0 | y1 | x2 | … |
fby is a delay operator. The expression x fby y, which can be read as “x followed by y” takes the first value of x at the first instant, then takes the previous value of y. In other words, it delays y by one instant, and is initialized by x.
| x | x0 | x1 | x2 | … |
| y | y0 | y1 | y2 | … |
| x fby y | x0 | y0 | y1 | … |
It is often needed to separate the delay from the initialization. This is done using the delay operator pre, and the initialization operator ->. pre x delays its argument x, and has an unspecified value (denoted here by nil) at the first instant. x -> y takes the first value of x at the first instant, then the current value of y. The expression x -> (pre y) is equivalent to x fby y.
| x | x0 | x1 | x2 | … |
| y | y0 | y1 | y2 | … |
| pre x | nil | x0 | x1 | … |
| x -> y | x0 | y1 | y2 | … |
The initialization check made by the compiler checks that the behavior of a program never depends on the value nil. See section 1.1.10 for details.
Warning: A common error with the initialization
operator is to use it for defining the first two values of a
stream. This does not work, since x -> y -> z =
x -> z. One should instead write x fby y fby z or,
x -> pre (y -> pre z).
A program is made of a sequence of declarations of global
values. let defines non recursive global values whereas
let rec define recursive global values. These global values may
be (infinite) constant streams or functions. For example:
let dt = 0.001 let g = 9.81
These declarations define two infinite constant streams dt and
g. The type and clock of each expression are infered, the
compiler can display them by using the option -i:
$ lucyc -i tutorial.ls val dt : float val dt :: static val g : float val g :: static
For each declaration, we get the inferred type and clock. Clocks will be explained further in a later part.
Only constant values can be defined globally, thus rejecting the following program:
let init = true -> false
Trying to compile this program, we get the following answer:
$ lucyc tutorial.ls File "tutorial.ls", line 1, characters 11-24: >let init = true -> false > ^^^^^^^^^^^^^ This expression should be combinatorial.
The right part of a global let declaration cannot contain any
delay operations. Definitions containing delays are sequential and
introduced by the notation node
(see 1.1.5).
Stream functions are separated into combinatorial and sequential functions. A function is combinatorial when its output at instant n depends only on its input at the same instant n.
The definition of combinatorial function uses the let notation seen previously. Consider, for example, the function computing the average of its two inputs. We directly give its type and clock signatures as computed by the compiler.
let average (x,y) = (x + y) / 2 val average : int * int -> int val average :: ’a * ’a -> ’a
This function get the type signature int * int -> int stating
that it takes two integer streams and returns an integer stream. Its
clock signature states that it is a length preserving function,
that is, it returns a value for every input.
Function definition can contain local declarations, introduced using either the where, or the let notation (see 1.1.7). For example the average function can be written:
let average (x,y) = o where o = (x + y) / 2 let average (x,y) = let o = (x + y) / 2 in o
As another example of combinatorial program, we end with the classical
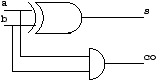
description of a one-bit adder. A full adder takes three bits
(a, b and a carry bit c) and it returns the
result c and the new carry co.
let xor (a, b) = (a & not(b)) or (not a & b)
let full_add(a, b, c) = (s, co) where
s = xor (xor (a, b), c)
and co = (a & b) or (b & c) or (a & c)
val xor : bool * bool -> bool
val xor :: ’a * ’a -> ’a
val full_add : bool * bool * bool -> bool * bool
val full_add :: ’a * ’a * ’a -> ’a * ’a
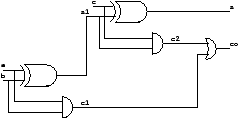
A full adder can be described more efficiently as a composition of two half adders. The graphical description is given in figure 1.1 and it corresponds to the following code:
let half_add(a,b) = (s, co)
where
s = xor (a, b)
and co = a & b
val half_add : bool * bool -> bool * bool
val half_add :: ’a * ’a -> ’a * ’a
let full_add(a,b,c) = (s, co)
where
rec (s1, c1) = half_add(a,b)
and (s, c2) = half_add(c, s1)
and co = c1 or c2
val full_add : bool * bool * bool -> bool * bool
val full_add :: ’a * ’a * ’a -> ’a * ’a * ’a
Sequential functions (or state functions) are such that their output at instant n may depend on the history of their inputs, that is, input values of instants k (k ≤ n).
To generalise, an expression is called sequential if it may produce a time evolving value when its free variables are kept constant. Otherwise, we call it combinatorial. A sufficient condition to be a combinatorial expression is not to contain any delay, initialization operator, nor state machine. This is verified by type checking.
Sequential functions are introduced by the keyword node. They receive
a different type signature than the one given to combinatorial functions.
The type signature int => int states that from is
a stream function from an integer stream to an integer stream and
that its output may depend on the history of its input.
The following function computes the sequence of integers starting at
some initial value given by parameter m:
let node from m = nat where rec nat = m -> pre nat + 1 val from : int => int val from :: ’a -> ’a
Applying this function to the constant stream 0 yields the following execution:
| m | 0 | 0 | 0 | 0 | 0 | 0 | … |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | … |
| pre nat | nil | 0 | 1 | 2 | 3 | 4 | … |
| pre nat + 1 | nil | 1 | 2 | 3 | 4 | 5 | … |
| m -> pre nat + 1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| from m | 0 | 1 | 2 | 3 | 4 | 5 | … |
Combinatorial functions are checked to be combinatorial at compile
time, thus forgetting the keyword node leads to an error:
let from n = nat where rec nat = n -> pre nat + 1
and we get:
$ lucyc tutorial.ls File "tutorial.ls", line 16, characters 12-28: > rec nat = n -> pre nat + 1 > ^^^^^^^^^^^^^^^^ This expression should be combinatorial.
We can define an edge detector in the following way:
let node edge c = c & not (false fby c)
| c | f | f | t | t | f | t | … |
| false | f | f | f | f | f | f | … |
| false fby c | f | f | f | t | t | f | … |
| not (false fby c) | t | t | t | f | f | t | … |
| edge c | f | f | t | f | f | t | … |
edge is a global function from boolean streams to
boolean streams.
An integrator is defined by:
let dt = 0.01 let node integr x0 dx = x where rec x = x0 -> pre x +. dx *. dt val integr : float -> float => float val integr :: ’a -> ’a -> ’a
integr is a global function returning a stream x defined
recursively. The operators +., *. stand for the addition
and multiplication over floating point numbers. Sequential functions
may be composed as any other functions. For example:
let node double_integr x0 dx0 d2x = x where rec x = integr x0 dx and dx = integr dx0 d2x
It is possible to build functions from other functions by applying the later only partially. For example:
let integr0 = integr 0.0
Which is equivalent to:
let node integr0 dx = integr 0.0 dx
Functions can be defined in an anonymous way and can be used as
values. Anonymous combinatorial functions are introduced using a
single arrow (->), anonymous sequential ones using a double
arrow (=>). For example, the expression fun x y -> x + y
is the sum function and has type int -> int -> int). The
expression fun x y => x fby x fby y defines a double delay and
has the type 'a -> 'a => 'a.
The functions average and from can be defined as:
let average = fun (x,y) -> (x + y) / 2 let from = fun n => nat where rec nat = n -> pre nat + 1
Variables may be defined locally with a let/in or
let rec/in and there is no special restriction on the
expressions appearing on the right of a definition. The following
program, computes the Euclidean distance between two points:
let distance (x0,y0) (x1,y1) = let d0 = x1 -. x0 in let d1 = y1 -. x1 in sqrt (d0 *. d0 +. d1 *. d1)
Notice that because d0 and d1 denote infinite sequences,
the computations of x1 -. x0 and y1 -. x1 are
(virtually) executed in parallel. Nonetheless, when writing sequences
of definitions let/in such as above, the sequential order is
preserved for each reaction of the system, that is, the current value
of d0 is always computed before the current value of
d1. This sequential order may be of importance if side-effects
are present.
Streams may be defined as a set of mutually recursive equations. The
function which computes the minimum and maximum of some input sequence
x can be written in (at least) the three equivalent ways:
let node min_max x = (min, max) where
rec min = x -> if x < pre min then x else pre min
and max = x -> if x > pre max then x else pre max
let node min_max x =
let rec min = x -> if x < pre min then x else pre min
and max = x -> if x > pre max then x else pre max in
(min, max)
let node min_max x = (min, max) where
rec (min, max) = (x, x) -> if x < pre min then (x, pre max)
else if x > pre max then (pre min, x)
else (pre min, pre max)
The classical sinus and co-sinus functions can be defined like the following:
let node sin_cos theta = (sin, cos) where
rec sin = theta *. integr 0.0 cos
and cos = theta *. integr 1.0 (0.0 -> -. (pre sin))
We end with the programming of a mouse controller, a very classical example. Its specification is the following:
Return the eventdoublewhen twoclickhas been received in less than fourtop. Emitssimpleif only one click has been received.
And here is a possible implementation:
(* counts the number of events from the last reset res *)
let node counter (res,event) = count where
rec count = if res then 0 else x
and x = 0 -> if event then pre count + 1 else pre count
let node mouse (click,top) = (single,double) where
rec counting = click -> if click & not (pre counting) then true
else if res & pre counting then false
else pre counting
and count = counter(res,top & counting)
and single = ((0 fby count) = 3) & top & not click
and double = (false fby counting) & click
and res = single or double
The language provides an alternative way to the use of the delay
pre in order to refer to the previous value of a stream. If
o is a stream variable defined by some equation, last o
refers to the last value of o. For example:
let node counter i = o where rec last o = i and o = last o + 1
The equation last o = i defines the memory last o.
This memory is initialized with the first value of i and then,
contains the previous value of o. The above program is thus
equivalent to the following one 1:
let node counter i = o where rec last_o = i -> pre o and o = last_o + 1
The memory last o will play an important role when combined
with control structures. This will be detailed later.
From a syntactical point of view, last is not an
operator: last o denotes a shared memory and the argument of
last is necessarily a name. Thus the following program:
let node f () = o where rec o = 0 -> last (o + 1)
is rejected and we get:
File "tutorial.ls", line 55, characters 21-22: > rec o = 0 -> last (o + 1) > ^ Syntax error.
Recursively defined values must not contain any instantaneous or causality loops in order to be able to compute values in a sequential way. For example, if we type:
let node from m = nat where rec nat = m -> nat + 1
the compiler emits the message:
File "tutorial.ls", line 35, characters 12-24: > rec nat = m -> nat + 1 > ^^^^^^^^^^^^ This expression may depend instantaneously of itself.
This program cannot be computed as nat depends on nat instantaneously.
The compiler statically reject program which cannot be scheduled
sequentially, that is streams whose value at instant n may depend on
some value at instant n. In practice, it imposes that any loop
crosses a delay pre or fby.
In the current version of the compiler, the causality analysis reject recursions which are not explicitely done through a delay. The following program (which is semantically correct) is rejected:
let node f x = 0 -> pre (x + 1) let node wrong () = let rec o = f o in o
The compiler checks that every delay operator is initialized. For example:
let node from m = nat where rec nat = pre nat + 1 File "tutorial.ls", line 35, characters 12-23: > rec nat = pre nat + 1 > ^^^^^^^^^^^ This expression may not be initialised.
The analysis is a one-bit analysis where expressions are
considered to be either always defined or always defined except at the
very first instant. It is precisely defined in [3]. In
practice, it rejects expressions like pre (pre e), that is,
un-initialized expressions cannot be used as an argument of a delay
and must be first initialized using ->.

