TP3 : Codage de Huffman

Le codage de Huffman peut être utilisé pour comprimer une suite d'éléments (par exemple un texte, qui est une suite de caractères) en remplaçant chaque élément par son code, qui est une séquence de valeurs booléennes. On s'intéressera ici à coder et décoder des suites de char.

1. Présentation

L'arbre de décodage est un arbre binaire dont les feuilles sont étiquetés par des caractères. Chaque feuille (caractère) est codée par une séquence binaire de la façon suivante : le chemin qui va de la racine de l'arbre à une feuille peut être représenté par la liste des choix 0 (sous-arbre de gauche) ou 1 (sous-arbre de droite) effectués a chaque noeud interne. Ceci définit une injection de l'ensemble des feuilles de l'arbre dans l'ensemble des séquences binaires.
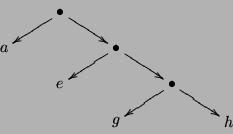
Appelons ensemble des codes valides l'image de cette injection. Par exemple, le dessin suivant représente un arbre avec des char sur les feuilles. Pour cet arbre, la liste 110 est un code valide qui représente la feuille g. Par contre, les listes 11 et 100 ne sont pas des codes valides.

L'encodage consiste à construire un bon arbre de décodage en fonction des fréquences des caractères du fichier à compresser, puis à produire la séquence binaire codée correspondant à la suite de caractères et à l'arbre. Le choix du bon arbre sera expliqué au paragraphe 4.

2. Manipulation d'arbres binaires

typedef struct chararbre {
  char data;
  struct chararbre *gauche;
  struct chararbre *droite;
} *arbre;

Réalisez les fonctions suivantes :

1. Les constructeurs du type arbre :
   • arbre feuille(char c);
   • arbre noeud(char c, arbre g, arbre d);
2. int est_feuille(arbre a); teste si on est en bout d'arbre
3. Vous n'aurez normalement pas besoin du destructeur du type arbre (le contraire du constructeur, qui donne les valeurs d'un noeud et libère sa mémoire, de façon à parcourir l'arbre en le détruisant au fur et à mesure). Vous allez donc vous contenter de void libere_arbre(arbre a); qui libère un arbre entier. C'est une fonction à utiliser avec précaution. Une bonne habitude, c'est de mettre les valeurs des variables qui pointaient sur l'arbre à NULL après la libération. La fonction void libere_arbre(arbre *p); pourrait le faire toute seule...
4. void imprime_arbre(arbre a); imprime un arbre. Comme on ne veut pas s'embêter avec une interface graphique, on propose d'utiliser une fonction auxiliaire void imprime_avec_blancs(arbre a, int b); qui affiche un arbre en mettant b espaces au début de son fils droit, et qui fait un parcours infixe de l'arbre.
   

   Par exemple, l'arbre 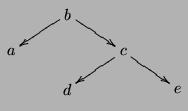sera affiché :

   b a c d e

5. Testez ces fonctions... (corrigé)

3. Décodage et encodage

typedef struct charliste { char data; struct charliste *suivant; } *sequence;

Réalisez les fonctions suivantes :

1. Le constructeur du type sequence, et sa fonction de libération de mémoire (ici encore, le destructeur devrait être inutile).
2. sequence decode_un(arbre h, sequence b); qui affiche l'élément codé en tête de b et retourne la suite de b. Par exemple, decode_un appliqué à l'arbre du début et à la séquence 1100 affiche g et retourne la séquence 0.
3. void decode(arbre h, sequence b); qui affiche la suite de caractères codés par b d'après l'arbre de codage h.
4. int code_un(arbre h, char c, sequence *b); qui ajoute à *b la séquence correspondant au caractère c dans h. La valeur de retour de la fonction est 0 (faux) si h ne contient pas c.
5. sequence code(arbre h, char *mot); qui retourne la sequence codée de la chaîne de caractères mot selon l'arbre de codage h. On rappelle que par convention les chaînes de caractères en C se terminent par le caractère '\0'.
6. N'oubliez pas de tester vos fonctions (corrigé)

4. Construction de l'arbre de codage

Le codage de Huffman est efficace si l'arbre de départ est bien choisi : il faut placer les éléments souvent rencontrés le plus proches possible de la racine. On va définir les types ci-dessous :

struct arbrepoids { arbre element; int poids; };
typedef struct liste { struct arbrepoids data; struct liste *suivant; } *liste;

On commence par fabriquer une liste L de la forme [(<elem₁>, poids₁); ...; (<elem_n>, poids_n)], où les elem_i sont les éléments qui doivent apparaître dans l'arbre de Huffman, et les poids_i représentent leur fréquence probable dans les textes à comprimer. La notation <elem_i> représente l'arbre à un seul noeud étiqueté par elem_i.

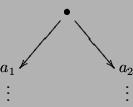
Il est facile de construire un arbre de Huffman optimal contenant les elem_i : On suppose que la liste est triée par poids croissants. L'algorithme suivant permet de construire un arbre optimal : On choisit dans la liste deux arbres a₁ et a₂ de poids p₁ et p₂ minimaux. On construit l'arbre A suivant :

On lui donne le poids p₁ + p₂, et on considère alors la liste de départ, moins les couples (a₁, p₁) et (a₂, p₂), plus (A, p₁ + p₂) insérée comme il faut pour préserver l'ordre des poids. Cette nouvelle liste contient un élément de moins que la précédente. On applique à nouveau la transformation jusqu'à obtenir une liste réduite à un seul couple. Elle contient l'arbre optimal.

Réalisez les fonctions suivantes :

1. Le constructeur du type liste, qui insère le nouvel élément en gardant la liste triée, et le destructeur, qui enlève un élément de poids minimal (en tête de liste, donc).
2. arbre make_huff(liste l); prend une liste en argument, et retourne un arbre de Huffman optimal pour cette liste.
3. liste make_liste(char[] chaine); construit la liste de fréquence des caractères de chaine (celle qui sera utilisée pour faire l'arbre de Huffman).
4. Programmez la fonction qui prend une chaîne de caractères et retourne le codage de Huffman optimal pour cette chaîne. Il faudra écrire le type correspondant.

5. Questions supplémentaires

1. Comment améliorer l'utilisation du type sequence pour gagner de la place ?
2. Écrivez le programme qui prend un fichier et produit dans un autre fichier son encodage de Huffman.