Alessandro Rudi
Researcher at INRIA and École Normale Supérieure, Paris
PI of the ERC starting grant REAL

Researcher at INRIA and École Normale Supérieure, Paris

Opensource Library in Python + PyTorch + CUDA, implementing the Falkon algorithm for multicore and multi-GPU architectures. Falkon allows to perform efficient and accurate supervised learning on large scale datasets of billions of examples. The algorithm is introduced in this paper and further improved in this paper. In this work we extended the algorithm to cover generalized self-concordant loss functions and finally in this paper we adapted it carefully to multi-GPU architectures, allowing it to scale up easily on datasets of billions of examples.
pdf code slides video@inproceedings{meanti2020kernel,
title={Kernel methods through the roof: handling billions of points efficiently},
author={Meanti, Giacomo and Carratino, Luigi and Rosasco, Lorenzo and Rudi, Alessandro},
booktitle={Arxiv preprint arXiv:2006.10350},
year={2020}
}
Opensource Library in MATLAB + CUDA, implementing the Falkon algorithm for multicore and single GPU architectures. Falkon allows to perform efficient and accurate supervised learning on large scale datasets. The algorithm is introduced in this paper.
pdf code slides video@inproceedings{rudi2017falkon,
title={FALKON: An optimal large scale kernel method},
author={Rudi, Alessandro and Carratino, Luigi and Rosasco, Lorenzo},
booktitle={Advances in Neural Information Processing Systems},
pages={3891--3901},
year={2017}
}
Opensource Library in MATLAB, implementing the NYTRO algorithm for multicore architectures. NYTRO combines Nystrom approximation with early stopping providing fast solutions to non-parametric learning problems. The algorithm is introduced in this paper
pdf code slides video@inproceedings{camoriano2016nytro,
title={NYTRO: When subsampling meets early stopping},
author={Camoriano, Raffaello and Angles, Tom{\'a}s and Rudi, Alessandro and Rosasco, Lorenzo},
booktitle={Artificial Intelligence and Statistics},
pages={1403--1411},
year={2016}
}
Opensource Library in MATLAB, implementing the incremental algorithm introduced in this paper to solve empirical risk minimization with squared loss and Nystrom approximation.
pdf code slides video@incollection{rudi2015less,
title = {Less is More: Nystr\"{o}m Computational Regularization},
author = {Rudi, Alessandro and Camoriano, Raffaello and Rosasco, Lorenzo},
booktitle = {Advances in Neural Information Processing Systems 28},
editor = {C. Cortes and N. D. Lawrence and D. D. Lee and M. Sugiyama and R. Garnett},
pages = {1657--1665},
year = {2015},
publisher = {Curran Associates, Inc.},
url = {http://papers.nips.cc/paper/5936-less-is-more-nystrom-computational-regularization.pdf}
}
We propose a novel non-parametric learning paradigm for the identification of drift and diffusion coefficients of non-linear stochastic differential equations, which relies upon discrete-time observations of the state. The key idea essentially consists of fitting a RKHS-based approximation of the corresponding Fokker-Planck equation to such observations, yielding theoretical estimates of learning rates which, unlike previous works, become increasingly tighter when the regularity of the unknown drift and diffusion coefficients becomes higher. Our method being kernel-based, offline pre-processing may in principle be profitably leveraged to enable efficient numerical implementation.
pdf code slides video@article{bonalli2023non,
title={Non-Parametric Learning of Stochastic Differential Equations with Fast Rates of Convergence},
author={Bonalli, Riccardo and Rudi, Alessandro},
journal={arXiv preprint arXiv:2305.15557},
year={2023}
}
We consider the problem of decomposing a regular non-negative function as a sum of squares of functions which preserve some form of regularity. In the same way as decomposing non-negative polynomials as sum of squares of polynomials allows to derive methods in order to solve global optimization problems on polynomials, decomposing a regular function as a sum of squares allows to derive methods to solve global optimization problems on more general functions. As the regularity of the functions in the sum of squares decomposition is a key indicator in analyzing the convergence and speed of convergence of optimization methods, it is important to have theoretical results guaranteeing such a regularity. In this work, we show second order sufficient conditions in order for a p times continuously differentiable non-negative function to be a sum of squares of p-2 differentiable functions. The main hypothesis is that, locally, the function grows quadratically in directions which are orthogonal to its set of zeros. The novelty of this result, compared to previous works is that it allows sets of zeros which are continuous as opposed to discrete, and also applies to manifolds as opposed to open sets of R^d. This has applications in problems where manifolds of minimizers or zeros typically appear, such as in optimal transport, and for minimizing functions defined on manifolds.
pdf code slides video@article{marteau2022second,
title={Second order conditions to decompose smooth functions as sums of squares},
author={Marteau-Ferey, Ulysse and Bach, Francis and Rudi, Alessandro},
journal={arXiv preprint arXiv:2202.13729},
year={2022}
}
We consider the unconstrained optimization of multivariate trigonometric polynomials by the sum-of-squares hierarchy of lower bounds. We first show a convergence rate of O(1/s^2) for the relaxation with degree s without any assumption on the trigonometric polynomial to minimize. Second, when the polynomial has a finite number of global minimizers with invertible Hessians at these minimizers, we show an exponential convergence rate with explicit constants. Our results also apply to the minimization of regular multivariate polynomials on the hypercube.
pdf code slides video@article{bach2022exponential,
title={Exponential convergence of sum-of-squares hierarchies for trigonometric polynomials},
author={Bach, Francis and Rudi, Alessandro},
journal={arXiv preprint arXiv:2211.04889},
year={2022}
}
Handling an infinite number of inequality constraints in infinite-dimensional spaces occurs in many fields, from global optimization to optimal transport. These problems have been tackled individually in several previous articles through kernel Sum-Of-Squares (kSoS) approximations. We propose here a unified theorem to prove convergence guarantees for these schemes. Inequalities are turned into equalities to a class of nonnegative kSoS functions. This enables the use of scattering inequalities to mitigate the curse of dimensionality in sampling the constraints, leveraging the assumed smoothness of the functions appearing in the problem. This approach is illustrated in learning vector fields with side information, here the invariance of a set.
pdf code slides video@article{bach2022exponential,
title={Exponential convergence of sum-of-squares hierarchies for trigonometric polynomials},
author={Bach, Francis and Rudi, Alessandro},
journal={arXiv preprint arXiv:2211.04889},
year={2022}
}
We consider the global minimization of smooth functions based solely on function evaluations. Algorithms that achieve the optimal number of function evaluations for a given precision level typically rely on explicitly constructing an approximation of the function which is then minimized with algorithms that have exponential running-time complexity. In this paper, we consider an approach that jointly models the function to approximate and finds a global minimum. This is done by using infinite sums of square smooth functions and has strong links with polynomial sum-of-squares hierarchies. Leveraging recent representation properties of reproducing kernel Hilbert spaces, the infinite-dimensional optimization problem can be solved by subsampling in time polynomial in the number of function evaluations, and with theoretical guarantees on the obtained minimum. Given $n$ samples, the computational cost is $O(n^{3.5})$ in time, $O(n^2)$ in space, and we achieve a convergence rate to the global optimum that is $O(n^{-m/d + 1/2 + 3/d})$ where $m$ is the degree of differentiability of the function and $d$ the number of dimensions. The rate is nearly optimal in the case of Sobolev functions and more generally makes the proposed method particularly suitable for functions which have a large number of derivatives. Indeed, when $m$ is in the order of $d$, the convergence rate to the global optimum does not suffer from the curse of dimensionality, which affects only the worst case constants (that we track explicitly through the paper).
pdf code slides video@inproceedings{rudi2020global,
title={Finding Global Minima via Kernel Approximations},
author={Rudi, Alessandro and Marteau-Ferey, Ulysse and Bach, Francis},
year={2020},
booktitle={Arxiv preprint arXiv:2012.11978},
primaryClass={math.OC}
}
We consider the global minimization of smooth functions based solely on function evaluations. Algorithms that achieve the optimal number of function evaluations for a given precision level typically rely on explicitly constructing an approximation of the function which is then minimized with algorithms that have exponential running-time complexity. In this paper, we consider an approach that jointly models the function to approximate and finds a global minimum. This is done by using infinite sums of square smooth functions and has strong links with polynomial sum-of-squares hierarchies. Leveraging recent representation properties of reproducing kernel Hilbert spaces, the infinite-dimensional optimization problem can be solved by subsampling in time polynomial in the number of function evaluations, and with theoretical guarantees on the obtained minimum. Given $n$ samples, the computational cost is $O(n^{3.5})$ in time, $O(n^2)$ in space, and we achieve a convergence rate to the global optimum that is $O(n^{-m/d + 1/2 + 3/d})$ where $m$ is the degree of differentiability of the function and $d$ the number of dimensions. The rate is nearly optimal in the case of Sobolev functions and more generally makes the proposed method particularly suitable for functions which have a large number of derivatives. Indeed, when $m$ is in the order of $d$, the convergence rate to the global optimum does not suffer from the curse of dimensionality, which affects only the worst case constants (that we track explicitly through the paper).
pdf code slides video@inproceedings{rudi2020global,
title={Finding Global Minima via Kernel Approximations},
author={Rudi, Alessandro and Marteau-Ferey, Ulysse and Bach, Francis},
year={2020},
booktitle={Arxiv preprint arXiv:2012.11978},
primaryClass={math.OC}
}
It is well-known that plug-in statistical estimation of optimal transport suffers from the curse of dimensionality. Despite recent efforts to improve the rate of estimation with the smoothness of the problem, the computational complexities of these recently proposed methods still degrade exponentially with the dimension. In this paper, thanks to an infinite-dimensional sum-of-squares representation, we derive a statistical estimator of smooth optimal transport which achieves a precision ε from $Õ(ε^{−2})$ independent and identically distributed samples from the distributions, for a computational cost of $Õ (ε^{−4})$ when the smoothness increases, hence yielding dimension-free statistical and computational rates, with potentially exponentially dimension-dependent constants.
pdf code slides video@inproceedings{vacher2021dimensionfree,
title={A Dimension-free Computational Upper-bound for Smooth Optimal Transport Estimation},
author={Adrien Vacher and Boris Muzellec and Alessandro Rudi and Francis Bach and Francois-Xavier Vialard},
year={2021},
booktitle={Arxiv preprint arXiv:2012.11978},
primaryClass={math.ST}
}
Kernel methods provide an elegant and principled approach to nonparametric learning, but so far could hardly be used in large scale problems, since naïve implementations scale poorly with data size. Recent advances have shown the benefits of a number of algorithmic ideas, for example combining optimization, numerical linear algebra and random projections. Here, we push these efforts further to develop and test a solver that takes full advantage of GPU hardware. Towards this end, we designed a preconditioned gradient solver for kernel methods exploiting both GPU acceleration and parallelization with multiple GPUs, implementing out-of-core variants of common linear algebra operations to guarantee optimal hardware utilization. Further, we optimize the numerical precision of different operations and maximize efficiency of matrix-vector multiplications. As a result we can experimentally show dramatic speedups on datasets with billions of points, while still guaranteeing state of the art performance. Additionally, we make our software available as an easy to use library.
pdf code slides video@inproceedings{meanti2020kernel,
title={Kernel methods through the roof: handling billions of points efficiently},
author={Meanti, Giacomo and Carratino, Luigi and Rosasco, Lorenzo and Rudi, Alessandro},
booktitle={Arxiv preprint arXiv:2006.10350},
year={2020}
}
Linear models have shown great effectiveness and flexibility in many fields such as machine learning, signal processing and statistics. They can represent rich spaces of functions while preserving the convexity of the optimization problems where they are used, and are simple to evaluate, differentiate and integrate. However, for modeling non-negative functions, which are crucial for unsupervised learning, density estimation, or non-parametric Bayesian methods, linear models are not applicable directly. Moreover, current state-of-the-art models like generalized linear models either lead to non-convex optimization problems, or cannot be easily integrated. In this paper we provide the first model for non-negative functions which benefits from the same good properties of linear models. In particular, we prove that it admits a representer theorem and provide an efficient dual formulation for convex problems. We study its representation power, showing that the resulting space of functions is strictly richer than that of generalized linear models. Finally we extend the model and the theoretical results to functions with outputs in convex cones. The paper is complemented by an experimental evaluation of the model showing its effectiveness in terms of formulation, algorithmic derivation and practical results on the problems of density estimation, regression with heteroscedastic errors, and multiple quantile regression.
pdf code slides video@article{marteau2020nonnegative,
title={Non-parametric Models for Non-negative Functions},
author={Marteau-Ferey, Ulysse and Bach, Francis and Rudi, Alessandro},
journal={arXiv preprint arXiv:2007.03926},
year={2020}
}
We consider the setting of online logistic regression and consider the regret with respect to the 2-ball of radius B. It is known (see [Hazan et al., 2014]) that any proper algorithm which has logarithmic regret in the number of samples (denoted n) necessarily suffers an exponential multiplicative constant in B. In this work, we design an efficient improper algorithm that avoids this exponential constant while preserving a logarithmic regret. Indeed,[Foster et al., 2018] showed that the lower bound does not apply to improper algorithms and proposed a strategy based on exponential weights with prohibitive computational complexity. Our new algorithm based on regularized empirical risk minimization with surrogate losses satisfies a regret scaling as O (B log (Bn)) with a per-round time-complexity of order O (d^ 2).
pdf code slides video@article{jezequel2020efficient,
title={Efficient improper learning for online logistic regression},
author={J{\'e}z{\'e}quel, R{\'e}mi and Gaillard, Pierre and Rudi, Alessandro},
booktitle={Conference on Learning Theory (COLT)},
pages={to appear},
year={2020}
}
Max-margin methods for binary classification such as the support vector machine (SVM) have been extended to the structured prediction setting under the name of max-margin Markov networks (M3N), or more generally structural SVMs. Unfortunately, these methods are statistically inconsistent when the relationship between inputs and labels is far from deterministic. We overcome such limitations by defining the learning problem in terms of a "max-min" margin formulation, naming the resulting method max-min margin Markov networks (M4N). We prove consistency and finite sample generalization bounds for M4N and provide an explicit algorithm to compute the estimator. The algorithm achieves a generalization error of 1/sqrt(n) for a total cost of O(n) projection-oracle calls (which have at most the same cost as the max-oracle from M3N). Experiments on multi-class classification, ordinal regression, sequence prediction and matching demonstrate the effectiveness of the proposed method.
pdf code slides video@inproceedings{nowak2020consistent,
title={Consistent Structured Prediction with Max-Min Margin Markov Networks},
author={Alex Nowak-Vila, Francis Bach, Alessandro Rudi},
booktitle={International Conference of Machine Learning (ICML)},
pages={to appear},
year={2020}
}
Annotating datasets is one of the main costs in nowadays supervised learning. The goal of weak supervision is to enable models to learn using only forms of labelling which are cheaper to collect, as partial labelling. This is a type of incomplete annotation where, for each datapoint, supervision is cast as a set of labels containing the real one. The problem of supervised learning with partial labelling has been studied for specific instances such as classification, multi-label, ranking or segmentation, but a general framework is still missing. This paper provides a unified framework based on structured prediction and on the concept of infimum loss to deal with partial labelling over a wide family of learning problems and loss functions. The framework leads naturally to explicit algorithms that can be easily implemented and for which proved statistical consistency and learning rates. Experiments confirm the superiority of the proposed approach over commonly used baselines.
pdf code slides video@inproceedings{cabannes2020structured,
title={Structured Prediction with Partial Labelling through the Infimum Loss},
author={Vivien Cabannes, Alessandro Rudi, Francis Bach},
booktitle={International Conference of Machine Learning (ICML)},
pages={to appear},
year={2020}
}
Poincaré inequalities are ubiquitous in probability and analysis and have various applications in statistics (concentration of measure, rate of convergence of Markov chains). The Poincar {é} constant, for which the inequality is tight, is related to the typical convergence rate of diffusions to their equilibrium measure. In this paper, we show both theoretically and experimentally that, given sufficiently many samples of a measure, we can estimate its Poincar {é} constant. As a by-product of the estimation of the Poincar {é} constant, we derive an algorithm that captures a low dimensional representation of the data by finding directions which are difficult to sample. These directions are of crucial importance for sampling or in fields like molecular dynamics, where they are called reaction coordinates. Their knowledge can leverage, with a simple conditioning step, computational bottlenecks by using importance sampling techniques.
pdf code slides video@inproceedings{pillaud2020statistical,
title={Gain with no Pain: Efficient Kernel-PCA by Nyström Sampling},
author={Sterge, Nicholas and Sriperumbudur, Bharath and Rosasco, Lorenzo and Rudi, Alessandro},
booktitle={Artificial Intelligence and Statistics},
pages={to appear},
year={2020}
}
In this paper, we propose and study a Nyström based approach to efficient large scale kernel principal component analysis (PCA). The latter is a natural nonlinear extension of classical PCA based on considering a nonlinear feature map or the corresponding kernel. Like other kernel approaches, kernel PCA enjoys good mathematical and statistical properties but, numerically, it scales poorly with the sample size. Our analysis shows that Nyström sampling greatly improves computational efficiency without incurring any loss of statistical accuracy. While similar effects have been observed in supervised learning, this is the first such result for PCA. Our theoretical findings, which are also illustrated by numerical results, are based on a combination of analytic and concentration of measure techniques. Our study is more broadly motivated by the question of understanding the interplay between statistical and computational requirements for learning.
pdf code slides video@inproceedings{sterge2020gain,
title={Gain with no Pain: Efficient Kernel-PCA by Nyström Sampling},
author={Sterge, Nicholas and Sriperumbudur, Bharath and Rosasco, Lorenzo and Rudi, Alessandro},
booktitle={Artificial Intelligence and Statistics},
pages={to appear},
year={2020}
}
Kriging is one of the most widely used emulation methods in simulation. However, memory and time requirements potentially hinder its application to datasets generated by high-dimensional simulators. We borrow from the machine learning literature to propose a new algorithmic implementation of kriging that, while preserving prediction accuracy, notably reduces time and memory requirements. The theoretical and computational foundations of the algorithm are provided. The work then reports results of extensive numerical experiments to compare the performance of the proposed algorithm against current kriging implementations, on simulators of increasing dimensionality. Findings show notable savings in time and memory requirements that allow one to handle inputs in more that \(10,000\) dimensions.
pdf code slides video@article{lu2020faster,
title={Faster Kriging: Facing High-Dimensional Simulators},
author={Lu, Xuefei and Rudi, Alessandro and Borgonovo, Emanuele and Rosasco, Lorenzo},
journal={Operations Research},
volume={68},
number={1},
pages={233--249},
year={2020},
publisher={INFORMS}
}
In this paper, we study regression problems over a separable Hilbert space with the square loss, covering non-parametric regression over a reproducing kernel Hilbert space. We investigate a class of spectral-regularized algorithms, including ridge regression, principal component analysis, and gradient methods. We prove optimal, high-probability convergence results in terms of variants of norms for the studied algorithms, considering a capacity assumption on the hypothesis space and a general source condition on the target function. Consequently, we obtain almost sure convergence results with optimal rates. Our results improve and generalize previous results, filling a theoretical gap for the non-attainable cases.
pdf code slides video@article{lin2020optimal,
title={Optimal rates for spectral algorithms with least-squares regression over hilbert spaces},
author={Lin, Junhong and Rudi, Alessandro and Rosasco, Lorenzo and Cevher, Volkan},
journal={Applied and Computational Harmonic Analysis},
year={2020},
publisher={Elsevier}
}
We propose and analyze a novel theoretical and algorithmic framework for structured prediction. While so far the term has referred to discrete output spaces, here we consider more general settings, such as manifolds or spaces of probability measures. We define structured prediction as a problem where the output space lacks a vectorial structure. We identify and study a large class of loss functions that implicitly defines a suitable geometry on the problem. The latter is the key to develop an algorithmic framework amenable to a sharp statistical analysis and yielding efficient computations. When dealing with output spaces with infinite cardinality, a suitable implicit formulation of the estimator is shown to be crucial.
pdf code slides video@article{ciliberto2020general,
author = {Ciliberto, Carlo and Rosasco, Lorenzo and Rudi, Alessandro},
title = {A General Framework for Consistent Structured Prediction with Implicit Loss Embeddings},
journal = {Journal of Machine Learning Research},
year = {2020},
volume = {21},
number = {98},
pages = {1-67},
url = {http://jmlr.org/papers/v21/20-097.html}
}
Simulating the time-evolution of quantum mechanical systems is BQP-hard and expected to be one of the foremost applications of quantum computers. We consider the approximation of Hamiltonian dynamics using subsampling methods from randomized numerical linear algebra. We propose conditions for the efficient approximation of state vectors evolving under a given Hamiltonian. As an immediate application, we show that sample based quantum simulation, a type of evolution where the Hamiltonian is a density matrix, can be efficiently classically simulated under specific structural conditions. Our main technical contribution is a randomized algorithm for approximating Hermitian matrix exponentials. The proof leverages the Nyström method to obtain low-rank approximations of the Hamiltonian. We envisage that techniques from randomized linear algebra will bring further insights into the power of quantum computation.
pdf code slides video@article{rudi2020approximating,
title={Approximating Hamiltonian dynamics with the Nystr{\"o}m method},
author={Rudi, Alessandro and Wossnig, Leonard and Ciliberto, Carlo and Rocchetto, Andrea and Pontil, Massimiliano and Severini, Simone},
journal={Quantum},
volume={4},
pages={234},
year={2020},
publisher={Verein zur F{\"o}rderung des Open Access Publizierens in den Quantenwissenschaften}
}
Within the framework of statistical learning theory it is possible to bound the minimum number of samples required by a learner to reach a target accuracy. We show that if the bound on the accuracy is taken into account, quantum machine learning algorithms for supervised learning—for which statistical guarantees are available—cannot achieve polylogarithmic runtimes in the input dimension. We conclude that, when no further assumptions on the problem are made, quantum machine learning algorithms for supervised learning can have at most polynomial speedups over efficient classical algorithms, even in cases where quantum access to the data is naturally available.
pdf code slides video@article{ciliberto2020statistical,
title={Statistical limits of supervised quantum learning},
author={Ciliberto, Carlo and Rocchetto, Andrea and Rudi, Alessandro and Wossnig, Leonard},
journal={Physical Review A},
volume={102},
number={4},
pages={042414},
year={2020},
publisher={APS}
}
We study the learning properties of nonparametric ridge-less least squares. In particular, we consider the common case of estimators defined by scale dependent kernels, and focus on the role of the scale. These estimators interpolate the data and the scale can be shown to control their stability through the condition number. Our analysis shows that are different regimes depending on the interplay between the sample size, its dimensions, and the smoothness of the problem. Indeed, when the sample size is less than exponential in the data dimension, then the scale can be chosen so that the learning error decreases. As the sample size becomes larger, the overall error stop decreasing but interestingly the scale can be chosen in such a way that the variance due to noise remains bounded. Our analysis combines, probabilistic results with a number of analytic techniques from interpolation theory.
pdf code slides video@inproceedings{pagliana2020interpolation,
title={Interpolation and Learning with Scale Dependent Kernels},
author={Pagliana, Nicol\'o and Rudi, Alessandro and De Vito, Ernesto and Rosasco, Lorenzo},
booktitle={Arxiv preprint arXiv:2006.09984},
year={2020}
}
We present a novel approach to image restoration that leverages ideas from localized structured prediction and non-linear multi-task learning. We optimize a penalized energy function regularized by a sum of terms measuring the distance between patches to be restored and clean patches from an external database gathered beforehand. The resulting estimator comes with strong statistical guarantees leveraging local dependency properties of overlapping patches. We derive the corresponding algorithms for energies based on the mean-squared and Euclidean norm errors. Finally, we demonstrate the practical effectiveness of our model on different image restoration problems using standard benchmarks.
pdf code slides video@inproceedings{eboli2020structured,
title={Structured and Localized Image Restoration},
author={Eboli, Thomas and Nowak-Vila, Alex and Sun, Jian and Bach, Francis and Ponce, Jean and Rudi, Alessandro},
booktitle={Arxiv preprint arXiv:2006.09261},
year={2020}
}
In this paper, we study large-scale convex optimization algorithms based on the Newton method applied to regularized generalized self-concordant losses, which include logistic regression and softmax regression. We first prove that our new simple scheme based on a sequence of problems with decreasing regularization parameters is provably globally convergent, that this convergence is linear with a constant factor which scales only logarithmically with the condition number. In the parametric setting, we obtain an algorithm with the same scaling than regular first-order methods but with an improved behavior, in particular in ill-conditioned problems. Second, in the non parametric machine learning setting, we provide an explicit algorithm combining the previous scheme with Nystr\" om projections techniques, and prove that it achieves optimal generalization bounds with a time complexity of order O (n df), a memory complexity of order O (df^ 2) and no dependence on the condition number, generalizing the results known for least squares regression. Here n is the number of observations and df is the associated degrees of freedom. In particular, this is the first large-scale algorithm to solve logistic and softmax regressions in the non-parametric setting with large condition numbers and theoretical guarantees.
pdf code slides video@incollection{marteau2019globally,
title = {Globally Convergent Newton Methods for Ill-conditioned Generalized Self-concordant Losses},
author = {Marteau-Ferey, Ulysse and Bach, Francis and Rudi, Alessandro},
booktitle = {Advances in Neural Information Processing Systems 32},
pages = {7636--7646},
year = {2019},
publisher = {Curran Associates, Inc.}
}
Key to structured prediction is exploiting the problem structure to simplify the learning process. A major challenge arises when data exhibit a local structure (e.g., are made by "parts") that can be leveraged to better approximate the relation between (parts of) the input and (parts of) the output. Recent literature on signal processing, and in particular computer vision, has shown that capturing these aspects is indeed essential to achieve state-of-the-art performance. While such algorithms are typically derived on a case-by-case basis, in this work we propose the first theoretical framework to deal with part-based data from a general perspective. We derive a novel approach to deal with these problems and study its generalization properties within the setting of statistical learning theory. Our analysis is novel in that it explicitly quantifies the benefits of leveraging the part-based structure of the problem with respect to the learning rates of the proposed estimator.
pdf code slides video@incollection{ciliberto2018localized,
title = {Localized Structured Prediction},
author = {Ciliberto, Carlo and Bach, Francis and Rudi, Alessandro},
booktitle = {Advances in Neural Information Processing Systems 32},
pages = {7301--7311},
year = {2019},
publisher = {Curran Associates, Inc.}
}
We are interested in a framework of online learning with kernels for low-dimensional but large-scale and potentially adversarial datasets. Considering the Gaussian kernel, we study the computational and theoretical performance of online variations of kernel Ridge regression. The resulting algorithm is based on approximations of the Gaussian kernel through Taylor expansion. It achieves for \(d\)-dimensional inputs a (close to) optimal regret of order \(O((logn)^{d+1})\) with per-round time complexity and space complexity \(O((logn)^{2d})\). This makes the algorithm a suitable choice as soon as \(n \gg e^d\) which is likely to happen in a scenario with small dimensional and large-scale dataset.
pdf code slides video@incollection{jezequel2019efficient,
title = {Efficient online learning with kernels for adversarial large scale problems},
author = {J\'{e}z\'{e}quel, R\'{e}mi and Gaillard, Pierre and Rudi, Alessandro},
booktitle = {Advances in Neural Information Processing Systems 32},
pages = {9432--9441},
year = {2019},
publisher = {Curran Associates, Inc.},
url = {http://papers.nips.cc/paper/9140-efficient-online-learning-with-kernels-for-adversarial-large-scale-problems.pdf}
}
The Sinkhorn distance, a variant of the Wasserstein distance with entropic regularization, is an increasingly popular tool in machine learning and statistical inference. We give a simple, practical, parallelizable algorithm NYS-SINK, based on Nyström approximation, for computing Sinkhorn distances on a massive scale. As we show in numerical experiments, our algorithm easily computes Sinkhorn distances on data sets hundreds of times larger than can be handled by state-of-the-art approaches. We also give provable guarantees establishing that the running time and memory requirements of our algorithm adapt to the intrinsic dimension of the underlying data.
pdf code slides video@incollection{altschuler2018massively,
title = {Massively scalable Sinkhorn distances via the Nystr\"{o}m method},
author = {Altschuler, Jason and Bach, Francis and Rudi, Alessandro and Niles-Weed, Jonathan},
booktitle = {Advances in Neural Information Processing Systems 32},
pages = {4427--4437},
year = {2019},
publisher = {Curran Associates, Inc.}
}
We consider learning methods based on the regularization of a convex empirical risk by a squared Hilbertian norm, a setting that includes linear predictors and non-linear predictors through positive-definite kernels. In order to go beyond the generic analysis leading to convergence rates of the excess risk as \(O(1/\sqrt{n})\) from \(n\) observations, we assume that the individual losses are self-concordant, that is, their third-order derivatives are bounded by their second-order derivatives. This setting includes least-squares, as well as all generalized linear models such as logistic and softmax regression. For this class of losses, we provide a bias-variance decomposition and show that the assumptions commonly made in least-squares regression, such as the source and capacity conditions, can be adapted to obtain fast non-asymptotic rates of convergence by improving the bias terms, the variance terms or both.
pdf code slides video@InProceedings{marteau2019beyond,
title = {Beyond Least-Squares: Fast Rates for Regularized Empirical Risk Minimization through Self-Concordance},
author = {Marteau{-}Ferey, Ulysse and Ostrovskii, Dmitrii and Bach, Francis and Rudi, Alessandro},
booktitle = {Proceedings of the Thirty-Second Conference on Learning Theory},
pages = {2294--2340},
year = {2019},
editor = {Beygelzimer, Alina and Hsu, Daniel},
volume = {99},
series = {Proceedings of Machine Learning Research},
address = {Phoenix, USA},
month = {25--28 Jun},
publisher = {PMLR}}
In this work we provide an estimator for the covariance matrix of a heavy-tailed random vector. We prove that the proposed estimator admits "affine-invariant" bounds of the form $$ (1+\epsilon) {\bf S} \preceq \widehat{\bf S} \preceq (1+\epsilon) {\bf S},$$ in high probability, where \(\bf S\) is the unknown covariance matrix, and \(\preceq\) is the positive semidefinite order on symmetric matrices. The result only requires the existence of fourth-order moments, and allows for \(\epsilon = O(\sqrt{\kappa^4 d/n})\) where \(\kappa\) is some measure of kurtosis of the distribution, \(d\) is the dimensionality of the space, and \(n\) is the sample size. More generally, we can allow for regularization with level \(\lambda\), then \(\epsilon\) depends on the degrees of freedom number which is generally smaller than \(d\). The computational cost of the proposed estimator is essentially \(O(d^2n + d^3)\), comparable to the computational cost of the sample covariance matrix in the statistically interesting regime \(n \gg d\). Its applications to eigenvalue estimation with relative error and to ridge regression with heavy-tailed random design are discussed.
pdf code slides video@InProceedings{ostrovskii2019affine,
title = {Affine Invariant Covariance Estimation for Heavy-Tailed Distributions},
author = {Ostrovskii, Dmitrii M. and Rudi, Alessandro},
booktitle = {Proceedings of the Thirty-Second Conference on Learning Theory},
pages = {2531--2550},
year = {2019},
editor = {Beygelzimer, Alina and Hsu, Daniel},
volume = {99},
series = {Proceedings of Machine Learning Research},
address = {Phoenix, USA},
month = {25--28 Jun},
publisher = {PMLR}
}
The problem of devising learning strategies for discrete losses (eg, multilabeling, ranking) is currently addressed with methods and theoretical analyses ad-hoc for each loss. In this paper we study a least-squares framework to systematically design learning algorithms for discrete losses, with quantitative characterizations in terms of statistical and computational complexity. In particular we improve existing results by providing explicit dependence on the number of labels for a wide class of losses and faster learning rates in conditions of low-noise. Theoretical results are complemented with experiments on real datasets, showing the effectiveness of the proposed general approach
pdf code slides video@InProceedings{nowak2019sharp,
title = {Sharp Analysis of Learning with Discrete Losses},
author = {Nowak, Alex and Bach, Francis and Rudi, Alessandro},
booktitle = {Proceedings of Machine Learning Research},
pages = {1920--1929},
year = {2019},
editor = {Chaudhuri, Kamalika and Sugiyama, Masashi},
volume = {89},
series = {Proceedings of Machine Learning Research},
address = {},
month = {16--18 Apr},
publisher = {PMLR}
}
In this work we provide a theoretical framework for structured prediction that generalizes the existing theory of surrogate methods for binary and multiclass classification based on estimating conditional probabilities with smooth convex surrogates (eg logistic regression). The theory relies on a natural characterization of structural properties of the task loss and allows to derive statistical guarantees for many widely used methods in the context of multilabeling, ranking, ordinal regression and graph matching. In particular, we characterize the smooth convex surrogates compatible with a given task loss in terms of a suitable Bregman divergence composed with a link function. This allows to derive tight bounds for the calibration function and to obtain novel results on existing surrogate frameworks for structured prediction such as conditional random fields and quadratic surrogates.
pdf code slides video@article{nowak2019general,
title={A General Theory for Structured Prediction with Smooth Convex Surrogates},
author={Nowak-Vila, Alex and Bach, Francis and Rudi, Alessandro},
booktitle={Arxiv preprint arXiv:1902.01958},
year={2019}
}
Computing the quadratic transportation metric (also called the 2-Wasserstein distance or root mean square distance) between two point clouds, or, more generally, two discrete distributions, is a fundamental problem in machine learning, statistics, computer graphics, and theoretical computer science. A long line of work has culminated in a sophisticated geometric algorithm due to [1], which runs in time \(O(n^{3/2})\), where \(n\) is the number of points. However, obtaining faster algorithms has proven difficult since the 2-Wasserstein distance is known to have poor sketching and embedding properties, which limits the effectiveness of geometric approaches. In this paper, we give an extremely simple deterministic algorithm with \(\tilde{O}(n)\) runtime by using a completely different approach based on entropic regularization, approximate Sinkhorn scaling, and low-rank approximations of Gaussian kernel matrices. We give explicit dependence of our algorithm on the dimension and precision of the approximation.
pdf code slides video@article{altschuler2018approximating,
title={Approximating the quadratic transportation metric in near-linear time},
author={Altschuler, Jason and Bach, Francis and Rudi, Alessandro and Weed, Jonathan},
journal={Arxiv preprint arXiv:1810.10046},
year={2018}
}
Sketching and stochastic gradient methods are arguably the most common techniques to derive efficient large scale learning algorithms. In this paper, we investigate their application in the context of nonparametric statistical learning. More precisely, we study the estimator defined by stochastic gradient with mini batches and random features. The latter can be seen as form of nonlinear sketching and used to define approximate kernel methods. The considered estimator is not explicitly penalized/constrained and regularization is implicit. Indeed, our study highlight how different parameters, such as number of features, iterations, step-size and mini-batch size control the learning properties of the solutions. We do this by deriving optimal finite sample bounds, under standard assumptions. The obtained results are corroborated and illustrated by numerical experiments.
pdf code slides video@inproceedings{carratino2018learning,
title={Learning with sgd and random features},
author={Carratino, Luigi and Rudi, Alessandro and Rosasco, Lorenzo},
booktitle={Advances in Neural Information Processing Systems},
pages={10212--10223},
year={2018}
}
Structured prediction provides a general framework to deal with supervised problems where the outputs have semantically rich structure. While classical approaches consider finite, albeit potentially huge, output spaces, in this paper we discuss how structured prediction can be extended to a continuous scenario. Specifically, we study a structured prediction approach to manifold valued regression. We characterize a class of problems for which the considered approach is statistically consistent and study how geometric optimization can be used to compute the corresponding estimator. Promising experimental results on both simulated and real data complete our study.
pdf code slides video@inproceedings{rudi2018manifold,
title={Manifold Structured Prediction},
author={Rudi, Alessandro and Ciliberto, Carlo and Marconi, GianMaria and Rosasco, Lorenzo},
booktitle={Advances in Neural Information Processing Systems},
pages={5611--5622},
year={2018}
}
Applications of optimal transport have recently gained remarkable attention thanks to the computational advantages of entropic regularization. However, in most situations the Sinkhorn approximation of the Wasserstein distance is replaced by a regularized version that is less accurate but easy to differentiate. In this work we characterize the differential properties of the original Sinkhorn distance, proving that it enjoys the same smoothness as its regularized version and we explicitly provide an efficient algorithm to compute its gradient. We show that this result benefits both theory and applications: on one hand, high order smoothness confers statistical guarantees to learning with Wasserstein approximations. On the other hand, the gradient formula allows us to efficiently solve learning and optimization problems in practice. Promising preliminary experiments complement our analysis.
pdf code slides video@inproceedings{luise2018wasserstein,
title = {Differential Properties of Sinkhorn Approximation for Learning with Wasserstein Distance},
author = {Luise, Giulia and Rudi, Alessandro and Pontil, Massimiliano and Ciliberto, Carlo},
booktitle = {Advances in Neural Information Processing Systems 31},
pages = {5864--5874},
year = {2018},
}
Leverage score sampling provides an appealing way to perform approximate computations for large matrices. Indeed, it allows to derive faithful approximations with a complexity adapted to the problem at hand. Yet, performing leverage scores sampling is a challenge in its own right and further approximations are typically needed. In this paper, we study the problem of leverage score sampling for positive definite matrices defined by a kernel. Our contribution is twofold. First we provide a novel algorithm for leverage score sampling. We provide theoretical guarantees as well as empirical results proving that the proposed algorithm is currently the fastest and most accurate solution to this problem. Second, we analyze the properties of the proposed method in a downstream supervised learning task. Combining several algorithmic ideas, we derive the fastest solver for kernel ridge regression and Gaussian process regression currently available. Also in this case, theoretical findings are corroborated by experimental results.
pdf code slides video@inproceedings{rudi2018fast,
title={On fast leverage score sampling and optimal learning},
author={Rudi, Alessandro and Calandriello, Daniele and Carratino, Luigi and Rosasco, Lorenzo},
booktitle={Advances in Neural Information Processing Systems},
pages={5673--5683},
year={2018}
}
We consider stochastic gradient descent (SGD) for least-squares regression with potentially several passes over the data. While several passes have been widely reported to perform practically better in terms of predictive performance on unseen data, the existing theoretical analysis of SGD suggests that a single pass is statistically optimal. While this is true for low-dimensional easy problems, we show that for hard problems, multiple passes lead to statistically optimal predictions while single pass does not; we also show that in these hard models, the optimal number of passes over the data increases with sample size. In order to define the notion of hardness and show that our predictive performances are optimal, we consider potentially infinite-dimensional models and notions typically associated to kernel methods, namely, the decay of eigenvalues of the covariance matrix of the features and the complexity of the optimal predictor as measured through the covariance matrix. We illustrate our results on synthetic experiments with non-linear kernel methods and on a classical benchmark with a linear model.
pdf code slides video@inproceedings{pillaud2018statistical,
title = {Statistical Optimality of Stochastic Gradient Descent on Hard Learning Problems through Multiple Passes},
author = {Pillaud-Vivien, Loucas and Rudi, Alessandro and Bach, Francis},
booktitle = {Advances in Neural Information Processing Systems 31},
pages = {8125--8135},
year = {2018},
}
We consider binary classification problems with positive definite kernels and square loss, and study the convergence rates of stochastic gradient methods. We show that while the excess testing loss (squared loss) converges slowly to zero as the number of observations (and thus iterations) goes to infinity, the testing error (classification error) converges exponentially fast if low-noise conditions are assumed.
pdf code slides video@inproceedings{pillaud2017exponential,
author = {Pillaud-Vivien, Loucas and Rudi, Alessandro and Bach, Francis},
title = {Exponential Convergence of Testing Error for Stochastic Gradient Methods},
booktitle = {Conference On Learning Theory, {COLT} 2018, Stockholm, Sweden, 6-9 July 2018.},
pages = {250--296},
year = {2018}
}
We study the generalization properties of ridge regression with random features in the statistical learning framework. We show for the first time that \(O(1/\sqrt{n})\) learning bounds can be achieved with only \(O(\sqrt{n})\) random features rather than \(O(n)\) as suggested by previous results. Further, we prove faster learning rates and show that they might require more random features, unless they are sampled according to a possibly problem dependent distribution. Our results shed light on the statistical computational trade-offs in large scale kernelized learning, showing the potential effectiveness of random features in reducing the computational complexity while keeping optimal generalization properties.
pdf code slides video@inproceedings{rudi2017generalization,
title={Generalization properties of learning with random features},
author={Rudi, Alessandro and Rosasco, Lorenzo},
booktitle={Advances in Neural Information Processing Systems},
pages={3218--3228},
year={2017}
}
Kernel methods provide a principled way to perform non linear, nonparametric learning. They rely on solid functional analytic foundations and enjoy optimal statistical properties. However, at least in their basic form, they have limited applicability in large scale scenarios because of stringent computational requirements in terms of time and especially memory. In this paper, we take a substantial step in scaling up kernel methods, proposing FALKON, a novel algorithm that allows to efficiently process millions of points. FALKON is derived combining several algorithmic principles, namely stochastic projections, iterative solvers and preconditioning. Our theoretical analysis shows that optimal statistical accuracy is achieved requiring essentially \(O(n)\) memory and \(O(n \sqrt{n})\) time. Extensive experiments show that state of the art results on available large scale datasets can be achieved even on a single machine.
pdf code slides video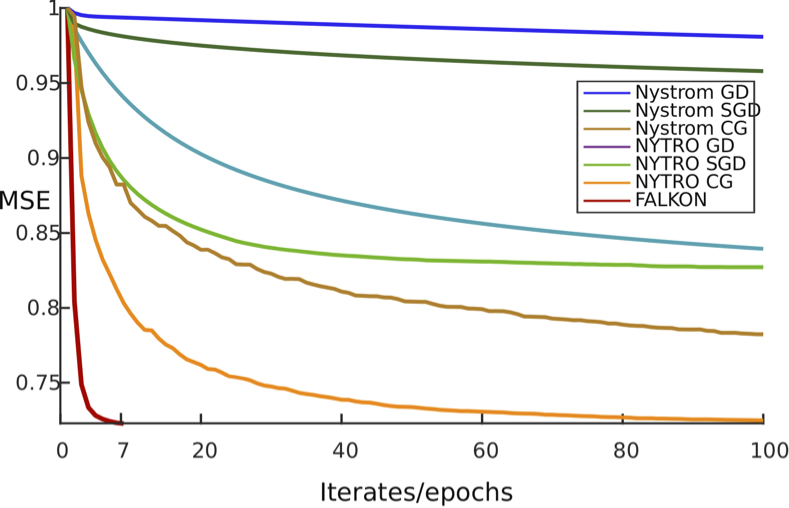
@inproceedings{rudi2017falkon,
title={FALKON: An optimal large scale kernel method},
author={Rudi, Alessandro and Carratino, Luigi and Rosasco, Lorenzo},
booktitle={Advances in Neural Information Processing Systems},
pages={3891--3901},
year={2017}
}
In the framework of non-parametric support estimation, we study the statistical properties of an estimator defined by means of Kernel Principal Component Analysis (KPCA). In the context of anomaly/novelty detection the algorithm was first introduced by Hoffmann in 2007. We also extend to above analysis to a larger class of set estimators defined in terms of a filter function.
pdf code slides video@article{rudi2017regularized,
author={Rudi, Alessandro and De Vito, Ernesto and Verri, Alessandro and Odone, Francesca},
title={Regularized Kernel Algorithms for Support Estimation},
journal={Frontiers in Applied Mathematics and Statistics},
volume={3},
pages={23},
year={2017},
doi={10.3389/fams.2017.00023}
}
Key to multitask learning is exploiting relationships between different tasks to improve prediction performance. If the relations are linear, regularization approaches can be used successfully. However, in practice assuming the tasks to be linearly related might be restrictive, and allowing for nonlinear structures is a challenge. In this paper, we tackle this issue by casting the problem within the framework of structured prediction. Our main contribution is a novel algorithm for learning multiple tasks which are related by a system of nonlinear equations that their joint outputs need to satisfy. We show that the algorithm is consistent and can be efficiently implemented. Experimental results show the potential of the proposed method.
pdf code slides video@inproceedings{ciliberto2017consistent,
title={Consistent Multitask Learning with Nonlinear Output Relations},
author={Ciliberto, Carlo and Rudi, Alessandro and Rosasco, Lorenzo and Pontil, Massimiliano},
booktitle={Advances in Neural Information Processing Systems},
pages={1983--1993},
year={2017}
}
We propose and analyze a regularization approach for structured prediction problems. We characterize a large class of loss functions that allows to naturally embed structured outputs in a linear space. We exploit this fact to design learning algorithms using a surrogate loss approach and regularization techniques. We prove universal consistency and finite sample bounds characterizing the generalization properties of the proposed method. Experimental results are provided to demonstrate the practical usefulness of the proposed approach.
pdf code slides video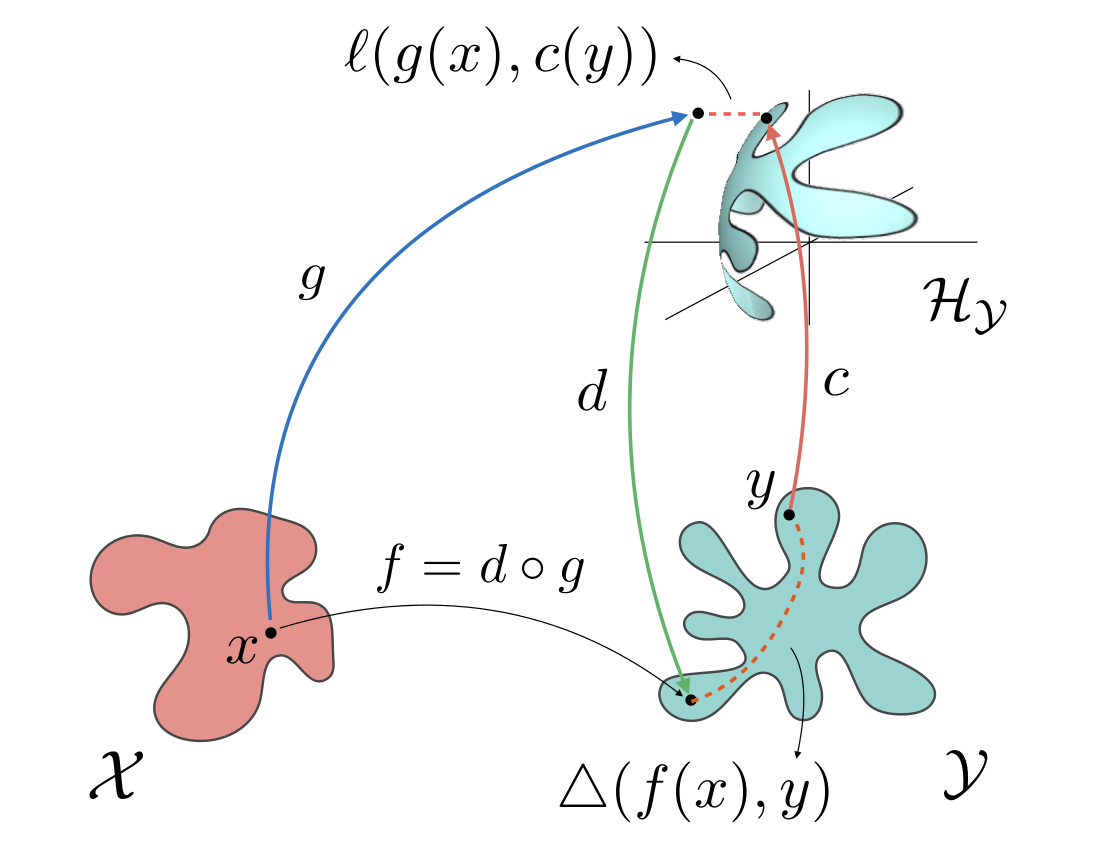
@inproceedings{ciliberto2016consistent,
title={A Consistent Regularization Approach for Structured Prediction},
author={Ciliberto, Carlo and Rosasco, Lorenzo and Rudi, Alessandro},
booktitle={Advances in Neural Information Processing Systems},
pages={4412--4420},
year={2016}
}
Early stopping is a well known approach to reduce the time complexity for performing training and model selection of large scale learning machines. On the other hand, memory/space (rather than time) complexity is the main constraint in many applications, and randomized subsampling techniques have been proposed to tackle this issue. In this paper we ask whether early stopping and subsampling ideas can be combined in a fruitful way. We consider the question in a least squares regression setting and propose a form of randomized iterative regularization based on early stopping and subsampling. In this context, we analyze the statistical and computational properties of the proposed method. Theoretical results are complemented and validated by a thorough experimental analysis.
pdf code slides video@inproceedings{camoriano2016nytro,
title={NYTRO: When subsampling meets early stopping},
author={Camoriano, Raffaello and Angles, Tom{\'a}s and Rudi, Alessandro and Rosasco, Lorenzo},
booktitle={Artificial Intelligence and Statistics},
pages={1403--1411},
year={2016}
}
We study Nystrom type subsampling approaches to large scale kernel methods, and prove learning bounds in the statistical learning setting, where random sampling and high probability estimates are considered. In particular, we prove that these approaches can achieve optimal learning bounds, provided the subsampling level is suitably chosen. These results suggest a simple incremental variant of Nystr\"om Kernel Regularized Least Squares, where the subsampling level implements a form of computational regularization, in the sense that it controls at the same time regularization and computations. Extensive experimental analysis shows that the considered approach achieves state of the art performances on benchmark large scale datasets.
pdf code slides video@incollection{rudi2015less,
title = {Less is More: Nystr\"{o}m Computational Regularization},
author = {Rudi, Alessandro and Camoriano, Raffaello and Rosasco, Lorenzo},
booktitle = {Advances in Neural Information Processing Systems 28},
editor = {C. Cortes and N. D. Lawrence and D. D. Lee and M. Sugiyama and R. Garnett},
pages = {1657--1665},
year = {2015},
publisher = {Curran Associates, Inc.},
url = {http://papers.nips.cc/paper/5936-less-is-more-nystrom-computational-regularization.pdf}
}
We consider here the classic problem of support estimation, or learning a set from random samples, and propose a natural but novel approach to address it. We do this by investigating its connection with a seemingly distinct problem, namely subspace learning.
pdf code slides video@incollection{rudi2014learning,
title={Learning Sets and Subspaces},
author={Rudi, Alessandro and Canas, G. D. and De Vito, Ernesto and Rosasco, Lorenzo},
booktitle={Regularization, Optimization, Kernels, and Support Vector Machines},
pages={337--357},
year={2014},
publisher={CRC Press}
}
In this paper we discuss the Spectral Support Estimation algorithm [1] by analyzing its geometrical and computational properties. The estimator is non-parametric and the model selection depends on three parameters whose role is clarified by simulations on a two-dimensional space. The performance of the algorithm for novelty detection is tested and compared with its main competitors on a collection of real benchmark datasets of different sizes and types.
pdf code slides video@article{rudi2014geometrical,
title={Geometrical and computational aspects of Spectral Support Estimation for novelty detection},
author={Rudi, Alessandro and Odone, Francesca and De Vito, Ernesto},
journal={Pattern Recognition Letters},
volume={36},
pages={107--116},
year={2014},
publisher={Elsevier}
}
A large number of algorithms in machine learning, from principal component analysis (PCA), and its non-linear (kernel) extensions, to more recent spectral embedding and support estimation methods, rely on estimating a linear subspace from samples. In this paper we introduce a general formulation of this problem and derive novel learning error estimates. Our results rely on natural assumptions on the spectral properties of the covariance operator associated to the data distribution, and hold for a wide class of metrics between subspaces. As special cases, we discuss sharp error estimates for the reconstruction properties of PCA and spectral support estimation. Key to our analysis is an operator theoretic approach that has broad applicability to spectral learning methods.
pdf code slides video@inproceedings{rudi2013sample,
title={On the sample complexity of subspace learning},
author={Rudi, Alessandro and Canas, Guillermo D and Rosasco, Lorenzo},
booktitle={Advances in Neural Information Processing Systems},
pages={2067--2075},
year={2013}
}
The process of model selection and assessment aims at finding a subset of parameters that minimize the expected test error for a model related to a learning algorithm. Given a subset of tuning parameters, an exhaustive grid search is typically performed. In this paper an automatic algorithm for model selection and assessment is proposed. It adaptively learns the error function in the parameters space, making use of scale space theory and statistical learning theory in order to estimate a reduced number of models and, at the same time, to make them more reliable. Extensive experiments are performed on the MNIST dataset.
pdf code slides video@inproceedings{rudi2012adaptive,
title={Adaptive Optimization for Cross Validation.},
author={Rudi, Alessandro and Chiusano, Gabriele and Verri, Alessandro},
booktitle={ESANN},
year={2012}
}
A novel approach to 3D gaze estimation for wearable multi-camera devices is proposed and its effectiveness is demonstrated both theoretically and empirically. The proposed approach, firmly grounded on the geometry of the multiple views, introduces a calibration procedure that is efficient, accurate, highly innovative but also practical and easy. Thus, it can run online with little intervention from the user. The overall gaze estimation model is general, as no particular complex model of the human eye is assumed in this work. This is made possible by a novel approach, that can be sketched as follows: each eye is imaged by a camera; two conics are fitted to the imaged pupils and a calibration sequence, consisting in the subject gazing a known 3D point, while moving his/her head, provides information to 1) estimate the optical axis in 3D world; 2) compute the geometry of the multi-camera system; 3) estimate the Point of Regard in 3D world. The resultant model is being used effectively to study visual attention by means of gaze estimation experiments, involving people performing natural tasks in wide-field, unstructured scenarios.
pdf code slides video@inproceedings{pirri2011general,
title={A general method for the point of regard estimation in 3D space},
author={Pirri, Fiora and Pizzoli, Matia and Rudi, Alessandro},
booktitle={Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on},
pages={921--928},
year={2011},
organization={IEEE}
}
The Viewing Graph [1] represents several views linked by the corresponding fundamental matrices, estimated pairwise. Given a Viewing Graph, the tuples of consistent camera matrices form a family that we call the Solution Set. This paper provides a theoretical framework that formalizes different properties of the topology, linear solvability and number of solutions of multi-camera systems. We systematically characterize the topology of the Viewing Graph in terms of its solution set by means of the associated algebraic bilinear system. Based on this characterization, we provide conditions about the linearity and the number of solutions and define an inductively constructible set of topologies which admit a unique linear solution. Camera matrices can thus be retrieved efficiently and large viewing graphs can be handled in a recursive fashion. The results apply to problems such as the projective reconstruction from multiple views or the calibration of camera networks.
pdf code slides video@inproceedings{rudi2010linear,
title={Linear solvability in the viewing graph},
author={Rudi, Alessandro and Pizzoli, Matia and Pirri, Fiora},
booktitle={Asian Conference on Computer Vision},
pages={369--381},
year={2010},
organization={Springer}
}

I am the PI of ERC starting grant REAL 'Reliable and cost-effective large scale machine learning' (1.5 millions €, 2021-2026). The project starts from the consideration that nowadays we are experiencing a new scenario where data are exponentially growing compared to the computational resources (post Moore’s law era), and ML algorithms are becoming crucial building blocks in complex systems for decision making, engineering, and science.
The criticality is that current machine learning is not suitable to deal with this new scenario, both from a theoretical and a practical viewpoint:
The goal of REAL is to lay the foundations of a solid theoretical and algorithmic framework for reliable and cost-effective large scale machine learning on modern computational architectures. In particular, REAL will extend the classical supervised learning framework to provide algorithms with two additional guarantees:
We are part of the larger INRIA team SIERRA . Besides me, the group currently consists of:
Ph. D. Students
Visiting Ph. D. Students
Post-docs
Alumni PhD: