


The language provides means to define state machines, as a way to describe directly control dominated systems. These state machines can be composed in parallel with regular equations or other state machines and can be arbitrarily nested.
In this tutorial, we first consider state machines where transitions are only made of boolean expressions. Then, we consider two important extensions of the basic model. The first one is the ability to build define state machines with parameterized states. The second one introduces the general form of transitions made of signal matching and boolean expressions.
An automaton is a collection of states and transitions. A state is made of a set of equations in the spirit of the Mode-automata by Maraninchi & Rémond. Two kinds of transitions are provided, namely weak and strong transitions and for each of them, it is possible to enter in the next state by reset or by history. One important feature of these state machines is that only one set of equations is executed during one reaction.
Here is a two state automaton illustrating strong preemption. The
function expect awaits x to be true and emits
true for the remaining instants.
(* await x to be true and then sustain the value *)
let node expect x = o where
automaton
S1 -> do o = false unless x then S2
| S2 -> do o = true done
end
val expect : bool => bool
val expect :: ’a -> ’a
This automaton is made of two states, each of them defining the value
of a shared variable o. The keyword unless
indicates that o is defined by the equation o = false
from state S1 while x is false. At the instant where
x is true, S2 becomes the active state for the remaining
instant. Thus, the following chronogram hold:
| x | false | false | true | false | false | true | … |
| expect x | false | false | true | true | true | true | … |
On the contrary, the following function emits false at the
instant where x is true and true for the remaining
instants, thus corresponding to regular Moore automata.
(* await x to be true and then sustain the value *)
let node expect x = o where
automaton
S1 -> do o = false until x then S2
| S2 -> do o = true done
end
val expect : bool => bool
val expect :: ’a -> ’a
| x | false | false | true | false | false | true | … |
| expect x | false | false | false | true | true | true | … |
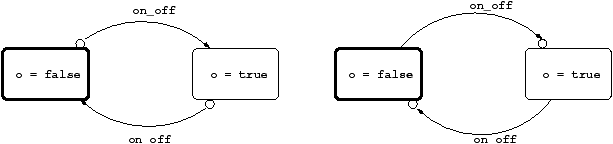
The classical two states switch automaton can be written like
the following:
let node weak_switch on_off = o where
automaton
False -> do o = false until on_off then True
| True -> do o = true until on_off then False
end
Note the difference with the following form with weak transitions only:
let node strong_switch on_off = o where
automaton
False -> do o = false unless on_off then True
| True -> do o = true unless on_off then False
end
We can check that for any boolean stream on_off, the following
property holds:
weak_switch on_off = strong_switch (false -> pre on_off)
The graphical representation of these two automata is given in figure 1.5.
Weak and strong conditions can be arbitrarily mixed as in the following variation of the switch automaton:
let node switch2 on_off stop = o where
automaton
False -> do o = false until on_off then True
| True -> do o = true until on_off then False unless stop then Stop
| Stop -> do o = true done
end
Compared to the previous version, state True can be strongly
preempted when some stop condition stop is true.
The ABRO example is due to Gérard Berry [2]. It highlight the expressive power of parallel composition and preemption in Esterel. The specification is the following:
Awaits the presence of eventsAandBand emitOat the exact instant where both events have been received. Reset this behavior every timeRis received.
Here is how we write it, replacing capital letters by small letter 7.
(* emit o and sustain it when a and b has been received *)
let node abo a b = (expect a) & (expect b)
(* here is ABRO: the same except that we reset the behavior *)
(* when r is true *)
let node abro a b r = o where
automaton
S1 -> do o = abo a b unless r then S1
end
The node abro is a one state automaton which resets the
computation of abo a b: every stream in abo a b restarts
with its initial value. The language provides a specific
reset/every primitive as a shortcut of such a one-state
automaton and we can write:
let node abro a b r = o where
reset
o = abo a b
every r
The reset/every construction combines a set of parallel
equations (separated with an and). Note that the reset
operation correspond to strong preemption: the body is reseted at the
instant where the condition is true. The language does not provide a
“weak reset”. Nonetheless, it can be easily obtained by inserting a
delay as illustrated below.
let node abro a b r = o where
reset
o = abo a b
every true -> pre r
It is possible to define names which are local to a state. These names can only be used inside the body of the state and may be used in weak conditions only.
The following programs integrates the integer sequence v and
emits false until the sum has reached some value max. Then, it
emits true during n instants.
let node consumme max n v = status where
automaton
S1 ->
let rec c = v -> pre c + v in
do status = false
until (c = max) then S2
| S2 ->
let rec c = 1 -> pre c + v in
do status = true
until (c = n) then S1
end
State S1 defines a local variable c which can be used to
compute the weak condition c = max and this does not introduce
any causality problem. Indeed, weak transitions are only effective
during the next reaction, that is, they define the next state, not the
current one. Moreover, there is no restriction on the kind of
expressions appearing in conditions and they may, in particular, have
some internal state. For example, the previous program can be
rewritten as:
let node counting v = cpt where
rec cpt = v -> pre cpt + v
let node consumme max n v = status where
automaton
S1 ->
do status = false
until (counting v = max) then S2
| S2 ->
do status = true
until (counting 1 = n) then S1
end
The body of a state is a sequence (possibly empty) of local
definitions (with let/in) followed by some definitions of
shared names (with do/until). As said previously, weak
conditions may depend on local names and shared names.
It is important to notice that using unless instead of
until leads to a causality error. Indeed, in a strong
preemption, the condition is evaluated before the equations of
the body and thus, cannot depend on them. In a weak preemption, the
condition is evaluated at the end, after the definitions of the
body have been evaluated. Thus, when writting:
let node consumme max n v = status where
automaton
S1 ->
let rec c = v -> pre c + v in
do status = false
unless (c = max) then S2
| S2 ->
let rec c = 1 -> pre c + v in
do status = true
unless (c = n) then S1
end
The compiler emits the message:
File "tutorial.ls", line 6: > unless c = max then S2 > ^^^^^^^ This expression may depend on itself.
In the previous examples, there is no communication between values
computed in each state. Consider a simple system made of two running
modes as seen previously. In the Up mode, the system increases
some value with a fixed step 1 whereas in the Down mode,
this value decreased with the same step. Now, the transition from one
mode to the other is described by a two-state automaton whose behavior
depends on the value computed in each mode. This example, due to
Maraninchi & Rémond [8] can be programmed in the
following way.
let node two_states i min max = o where
rec automaton
Up -> do
o = last o + 1
until (o = max) then Down
| Down -> do
o = last o - 1
until (o = min) then Up
end
and last o = i
An execution diagram is given below:
| i | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| min | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | … |
| max | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | … |
| last o | 0 | 1 | 2 | 3 | 4 | 3 | 2 | 1 | 0 | -1 | 0 | 1 | … |
| o | 1 | 2 | 3 | 4 | 3 | 2 | 1 | 0 | -1 | 0 | 1 | 2 | … |
| last o + 1 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | … | |||||
| last o - 1 | 3 | 2 | 1 | 0 | -1 | … |
The initial state can be used for defining some variables whose value can then be sustained in remaining states. In that case, their last value is considered to be defined. Moreover, it becomes possible not to define their value in all the states.
let node two_states i min max = o where
rec automaton
Init ->
do o = i until (i > 0) then Up
| Up ->
do o = last o + 1
until (o = max) then Down
| Down ->
do o = last o - 1
until (o = min) then Up
end
| i | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | … |
| min | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | … |
| max | 0 | 0 | 0 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | … |
| last o | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 3 | 2 | 1 | 0 | -1 | 0 | 1 | … |
| o | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 3 | 2 | 1 | 0 | -1 | 0 | 1 | 2 | … |
| last o + 1 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | … | |||||
| last o - 1 | 0 | 0 | 0 | 3 | 2 | 1 | 0 | -1 | … |
Because the initial state Init is only weakly preempted,
o is necessarily initialized with the current value of
i. Thus, last o is well defined in the remaining
states. Note that replacing the weak preemption by a strong one will
lead to an error.
let node two_states i min max = o where
rec automaton
Init ->
do o = i unless (i > 0) then Up
| Up ->
do o = last o + 1
until (o = max) then Down
| Down ->
do o = last o - 1
until (o = min) then Up
end
and we get:
File "tutorial.ls", line 128, characters 20-30: > o = last o + 1 > ^^^^^^^^^^ This expression may not be initialised.
We said previously that strong conditions must not depend on some
variables computed in the current state but they can depend on some
shared memory last o as in:
let node two_states i min max = o where
rec automaton
Init ->
do o = i until (i > 0) then Up
| Up ->
do o = last o + 1
unless (last o = max) then Down
| Down ->
do o = last o - 1
unless (last o = min) then Up
end
and we get the same execution diagram as before:
| i | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | … |
| min | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | … |
| max | 0 | 0 | 0 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | … |
| last o | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 3 | 2 | 1 | 0 | -1 | 0 | 1 | … |
| o | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 3 | 2 | 1 | 0 | -1 | 0 | 1 | 2 | … |
| last o + 1 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | … | |||||
| last o - 1 | 0 | 0 | 0 | 3 | 2 | 1 | 0 | -1 | … |
Note that the escape condition do x = 0 and y = 0 then Up in
the initial state is a shortcut for
do x = 0 and y = 0 until true then Up.
Finally, o do not have to be defined in all the states. In that
case, it keeps its previous value, that is, an equation
o = last o is implicitely added.
By default, when entering in a state, every computation in the state is reseted. We also provides some means to resume the internal memory of a state (this is called enter by history in UML diagrams).
let node two_modes min max = o where
rec automaton
Up -> do o = 0 -> last o + 1 until (o >= max) continue Down
| Down -> do o = last o - 1 until (o <= min) continue Up
end
| min | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | … |
| max | 0 | 0 | 0 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | … |
| o | 0 | -1 | 0 | 1 | 2 | 3 | 4 | 3 | 2 | 1 | 0 | -1 | 0 | 1 | 2 | … |
This is an other way to write activation conditions and is very convenient for programming a scheduler which alternate between some computations, each of them keeping its own state as in:
let node time_sharing c i = (x,y) where
rec automaton
Init ->
do x = 0 and y = 0 then S1
| S1 ->
do x = 0 -> pre x + 1 until c continue S2
| S2 ->
do y = 0 -> pre y + 1 until c continue S1
end


