


Up to now, we have only considered length preserving functions, that is, functions returning n items of their output when receiving n items of their input. We consider now a more general case allowing to sample stream and to compose them. This is achieved through the use of clocks.
when is a sampler that allows fast processes to communicate with slower ones by extracting sub-streams from streams according to a condition, i.e. a boolean stream.
| true | t | t | t | t | … |
| c | f | t | f | t | … |
| x | x0 | x1 | x2 | x3 | … |
| x when c | x1 | x3 | … | ||
| true on c | f | t | f | t | … |
The sampling operators introduce the notion of clock type. These clock types give some information about the time behavior of stream programs.
The clock of a stream s is a boolean sequence giving the
instants where s is defined. Among these clocks, the base clock
stands for the constant stream true: a stream on the base clock
is present at every instant. In the above example, the current value
of x when c is present when x and c are present
and c is true. Since x and c are on the base
clock true, the clock of x when c is noted
true on c.
Consider the sum function which make the sum of its input (that
is, sn = Σi = 0n xi).
let node sum x = s where rec s = x -> pre s + x
Now the sum function can be used at a slower rate by sampling
its input stream:
let node sampled_sum x y = sum(x when y) val sampled_sum : int -> bool => int val sampled_sum :: ’a -> (_c0:’a) -> ’a on _c0
sampled_sum has a function clock which follows its type
structure. This clock type says that for any clock 'a, if the
first argument of the function has clock 'a and the second
argument named _c0 has clock a, then the result is on
clock 'a on _c0 (every expression variable is renamed in the
clock to avoid name conflicts). An expression on clock
'a on _c0 is present when the clock 'a is true and the
boolean stream _c0 is present and true.
Now, the sampled sum can be instantiated with an actual clock. For example:
(* a counter that counts modulo n *) let node sample n = let rec cpt = 0 -> if pre cpt = n - 1 then 0 else pre cpt + 1 and ok = cpt = 0 in ok (* defining a 1/10 clock *) let clock ten = sample 10 (* sampling a sum on 1/10 *) let node sum_ten dx = sampled_sum dx ten val ten : bool val ten_hz :: ’a val sum_ten : int => int val sum_ten :: ’a -> ’a on ten
A clock name is introduced with the special keyword clock which builds
a clock from a boolean stream.
Warning:
Clocks provide a way to define control structures, that is,
pieces of code which are executed according to some condition. It is
thus important to understand their combination with delay operators as
exemplified in the diagram below:
| c | f | t | f | t | f | … |
| 1 | 1 | 1 | 1 | 1 | 1 | … |
| sum 1 | 1 | 2 | 3 | 4 | 5 | … |
| (sum 1) when c | 2 | 4 | … | |||
| 1 when c | 1 | 1 | … | |||
| sum (1 when c) | 1 | 2 | … | |||
| x | x0 | x1 | x2 | x3 | x4 | … |
| x when c | x1 | x3 | … | |||
| pre x | nil | x0 | x1 | x2 | x3 | … |
| pre (x when c) | nil | x1 | … | |||
| (pre x) when c | x0 | x2 | … |
As soon as a function f contains some delay operator, sampling its inputs is not equivalent to sampling its outputs, that is, f(x when c) ≠ (f x) when c.
Clocks can be arbitrarily nested. Consider, for example, the description of a (real) clock.
let clock sixty = sample 60 let node hour_minute_second second = let minute = second when sixty in let hour = minute when sixty in hour,minute,second val sixty : bool val sixty :: ’a val hour_minute_second : ’a => ’a * ’a * ’a val hour_minute_second :: ’a -> ’a on sixty on sixty * ’a on sixty * ’a
A stream on clock 'a on sixty on sixty is only present one
instant over 3600 instants which match perfectly what we are
expecting.
Warning: We make a special treatment for
clocks defined at top-level (as the clock sixty). A top-level
clock is defined by a boolean expression (combinatorial or sequential)
and is then considered as a constant process which can be instanciated
several times. In the above program, they are two instanciations of
the clock sixty: one is on some clock 'a whereas the
other run slowly at clock 'a on sixty.
merge conversely allows slow processes to communicate with faster ones by merging sub-streams into “larger” ones:
| c | f | t | f | f | f | t | … |
| x | x0 | x1 | … | ||||
| y | y0 | y1 | y2 | y3 | … | ||
| merge c x y | y0 | x0 | y1 | y2 | y3 | x1 | … |
For instance, the merge allows us to define an “holding”
function (the “current” operator of Lustre), which “holds” a
signal between two successive samples (here ydef is a default
value used before any sample has been taken):
let node hold ydef c x = y
where rec y = merge c x ((ydef -> pre y) whenot c)
val hold : ’a -> bool -> ’a => ’a
val hold :: ’a -> (_c0:’a) -> ’a on _c0 -> ’a
| c | f | t | f | f | f | t | … |
| x | x0 | x1 | … | ||||
| y | y0 | y1 | y2 | y3 | … | ||
| ydef | d0 | d1 | d2 | d3 | d4 | d5 | … |
| hold c x ydef | d0 | x0 | x0 | x0 | x0 | x1 | … |
Warning: Note the difference between merge and
if/then/else. merge composes two complementary sequences
and thus, has a lazy flavor. It is the data-flow version of the
classical (lazy) conditional of sequential programming languages. The
if/then/else is a strict operator which needs its three
arguments to be on the same clock 2.
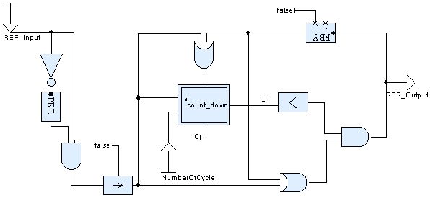
The following operator is a classical control engineering operator,
available in both the Scade/Lustre library and “digital” library of
Simulink. Its graphical representation in Scade/Lustre is given in
figure 1.2. This operator detects a rising edge (false to
true transition). The output becomes true as soon as a transition has
been detected and remains unchanged during number_of_cycle
cycles. The output is initially false and a rising edge occurring
while the output is true is detected. In Lucid Synchrone syntax, this is
written 3:
let node count_down (res, n) = cpt where
rec cpt = if res then n else (n -> pre (cpt - 1))
let node rising_edge_retrigger rer_input number_of_cycle = rer_output where
rec rer_output = (0 < v) & clk
and v = merge clk (count_down ((count,number_of_cycle) when clk))
((0 fby v) whenot clk)
and c = false fby rer_output
and clock clk = c or count
and count = false -> (rer_input & pre (not rer_input))
Using clocks defined globally, we can write simple over-sampling functions, i.e. functions whose output has a larger rate than the input. One simple example is the stuttering function which computes the sequence (on)n ∈ IN such that:
|
It is written as follows:
let clock half = h where rec h = true -> not (pre h) let node over x = hold 1 half x let node stuttering () = let rec nat = 0 -> pre nat + 1 in over nat val half : bool val half :: ’a val over : int => int val over :: ’a on half -> ’a val stuttering : unit => int val stuttering :: ’a -> ’b
This is an example of oversampling, that is, a function whose internal
clock (here 'a) is faster than the clock of its input
(here 'a on half): the function stuttering computes some
internal value whereas it does not receive any new input. It shows
that some limited form of oversampling — which is possible in
Signal and not in Lustre — can be achieved.
Figure 1.3: Duplication vs iteration for the computation of x5
Oversampling appear naturally in a system when considering program transformation and refinements. For example, when the architecture does not offer enough parallelism, we replace it by iteration and this has some consequence on the instant where the results become available. Consider, for example, the computation of the power of a sequence (yn)n ∈ IN such that:
|
Supposing that the machine is able to execute four multiplications, we simply write:
let node spower x = y where y = x * x * x * x * x let node shift_power x = y where y = 1 fby (x * x * x * x * x) val spower : int => int val spower :: ’a -> ’a val shift_power : int => int val shift_power :: ’a -> ’a
The graphical representation is given on the left of
figure 1.3. The output is available at the same
(logical) instant as the input is received and this is why the
function gets clock 'a -> 'a.
shift_power is another version obtained by inserting a delay
at the end of the computation. Now, a pipelined version can be
obtained by a simple retiming transformation, leading to a speed-up of
four in average.
let node ppower x = y where rec x2 = 1 fby x * x and px = 1 fby x and x3 = 1 fby x2 * px and ppx = 1 fby px and x4 = 1 fby x3 * ppx and pppx = 1 fby ppx and y = 1 fby x4 * pppx val ppower : int => int val ppower :: ’a -> ’a
| x | x0 | x1 | x2 | x3 | x4 | x5 | x6 | ... |
| spower x | x05 | x15 | x25 | x35 | x45 | x56 | x65 | ... |
| shift_power x | 1 | x05 | x15 | x25 | x35 | x45 | x56 | ... |
| ppower x | 1 | 1 | 1 | 1 | x05 | x15 | x25 | ... |
Now, suppose that the machine has only one multiplier
instead of four. Then, the value xn5 cannot be obtained in one
cycle. We replace parallel computation by iteration, making the clock
of x five times slower. The new system is given on the right of
figure 1.3.
let clock four = sample 4 let node tpower x = y where rec i = merge four x ((1 fby i) whenot four) and o = 1 fby (i * merge four x (o whenot four)) and y = o when four val tpower : int => int val tpower :: ’a on four -> ’a on four
| five | t | f | f | f | t | f | f | f | t | f | f | f | t | f | ... |
| x | x0 | x1 | x2 | x3 | ... | ||||||||||
| i | x0 | x0 | x0 | x0 | x1 | x1 | x1 | x1 | x2 | x2 | x2 | x2 | x3 | x3 | ... |
| o | 1 | x02 | x03 | x04 | x05 | x12 | x13 | x14 | x15 | x22 | x23 | x24 | x25 | x32 | ... |
| tpower x | 1 | x05 | x15 | x25 | ... |
spower x is a time refinement of the computation
of shift_power, it produces the same sequence of values. We
have made the internal clock faster than the input/output clock in
order to exhibit every step of the computation.
As a consequence of the clock discipline and clock inference, using
tpower in place of shift_power will automatically
slowdown the whole system. This guaranty modular design, that is,
tpower can be used anywhere power was previously used.
Remark: The current version of the compiler does
not take the value of clocks into account (that is, it is unable to
know that four is a periodic clock).
such that it can ensure the equivalence between the various designs.
x x0 x1 x2 x3 x4 x5 x6 ... half t f t f t f t ... x when half x0 x2 x4 x6 ... x & (x when half) x0 & x0 x1 & x2 x2 & x4 x3 & x6 ...
Figure 1.4: A non Synchronous Example
Program must follow some clocking rules. For example, the and gate
(&) expects its two arguments to be booleans and to be on the
same clock, as expressed by the following signatures:
val (&) : bool -> bool -> bool val (&) :: ’a -> ’a -> ’a
Thus, writting the following program leads to a clocking error:
let clock half = sample 2 let node odd x = x when half let node wrong_clocked x = x & odd x
where wrong_clocked x combines the stream x to the
sub-stream of x made by filtering one item over two. Thus it
should compute the sequence (xn & x2n)n∈IN. Note that
this computation is clearly not bounded memory through it is only
composed of bounded memory operators. The corresponding Kahn
network [6] of wrong_clocked x is depicted in
figure 1.4. Indeed & consumes one
item of its two inputs in order to produce one item of its output. One
of its two inputs is twice faster than the second one and, as time
goes on, the number of successive values to store in a buffer will
increase and the system will eventually stop. Whereas the sequence
(xn & x2n)n∈IN is perfectly well defined, it will be
considered as a non synchronous computation — its
corresponding Kahn Network cannot be executed without buffering —
and shall be statically rejected by the compiler. When given to the
compiler, we get:
File "tutorial.ls", line 78, characters 31-36: >let node wrong_clocked x = x & odd x > ^^^^^ This expression has clock ’a on half, but is used with clock ’a.
x gets clock 'b whereas odd x gets clock
'b on half and these two clocks cannot made be equal. Clock
constraints in Lucid Synchrone insure that the corresponding Kahn network can
be executed without synchronization mechanisms using possibly
unbounded buffering. This is why we reject it when dealing with
real-time applications.
When a clock name is introduced with the let clock
constructor, the name is considered to be unique
and does not take into account the expression on the right-hand side
of the let clock. Thus, the following program is rejected:
let node wrong () = let clock c = true in let v = 1 when c in let clock c = true in let w = 1 when c in v + w
and we get the following error:
File "tutorial.ls", line 62, characters 6-7: > v + w > ^ This expression has clock ’b on ?_c1, but is used with clock ’b on ?_c2.
Because of the inference aspect of the clock calculus, some restriction are imposed on the use of clocks 4. The main restriction is that it is not possible to return a value which depends on some clock computed locally 5.
When clocks are introduced with the clock constructions, these
clock must not escape their lexical scope. For example:
let node within min max x = o where rec clock c = (min <= x) & (x <= max) and o = true when c File "tutorial.ls", line 123-125, characters 4-75: >....node within min max x = o where > rec clock c = (min <= x) & (x <= max) > and o = true when c The clock of this expression, that is, ’b -> ’b on ?_c0 depends on ?_c0 which escape its scope.
This program is rejected because the let clock construction
introduces a fresh clock name ?_c0 which abstract the exact
value of c. This name must not exist already, that is, it must
not appear in the clock of some existing variable when clocking the
let/clock construct and it cannot escape its local scope.
Here, the program is rejected since the function returns an expression
on clock 'a on ?_c0 but ?_c0 must stay local to its
block structure.
let node escape x = let clock c = true in merge c (x + (1 when c)) 0 File "tutorial.ls", line 123-125, characters 4-75: >....node escape x = > let clock c = true in > merge c (x + (1 when c)) 0 The clock of this expression, that is, ’b on ?_c0 -> ’b depends on ?_c0 which escape its scope.
The program is rejected because the variable x should already
be on the clock 'a on ?_c0 in which ?_c0 appears. This
fresh name must not escape the scope of the construction.
Remark: Thus, clocks introduced by the
clock construction have a lifetime limited to their block.
This is an important restriction of Lucid Synchrone V3 whose clock calculus is
strictly less expressive than the one of V1. In this version (as well
as in Lustre), a function may return a value sampled on some boolean
value computed locally as soon as this value is also returned as an
output. This allows to eliminate the first type of scope
restriction. The program given above is simply written:
let node within min max x = (c, o) where rec clock c = (min <= x) & (x <= max) and o = true when c
Nonetheless, this is at a price of a more complex clock calculus and its usefullness in practice appeared to be questionnable. Moreover, one can often turn around this restriction by using signals as we shall see in section 1.5.


