Abstract Interpretation in a Nutshell

This introduction to static analysis by abstract interpretation has the objective of being simple, intuitive and informal. More technical introductions as well as bibliographic references are provided in [1,2,3].
A 30mn video (in French) can also be useful.

1.  Concrete semantics of programs

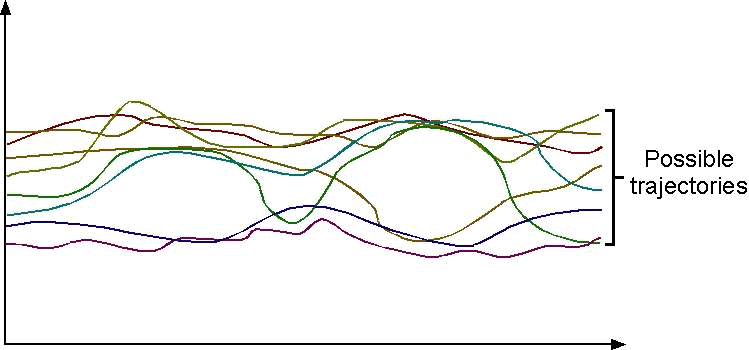
The concrete semantics of programs formalizes the set of all possible executions of this program in all possible execution environments. If an execution is represented by a curve showing the evolution of the vector x(t) of values of the input, state and output variables of the program as a function of the time t, this concrete semantics can be represented by a set of curves (with continuous time for short):
x(t)
t

2.  Undecidability

The concrete semantics of a program is an "infinite" mathematical object which is not computable: it is not possible to write a program able to represent and to compute all possible executions of any program in all its possible execution environments.

Hence, all non trivial questions about the concrete semantics of a program are undecidable: it is not possible to write a program able to answer any question about the possible executions of any program (since the concrete semantics of this program would have to be computable).

The mathematical analogy is that there is no theorem prover able, for example, to prove any theorem of arithmetics without human assistance.

3.  Specification of Safety Properties

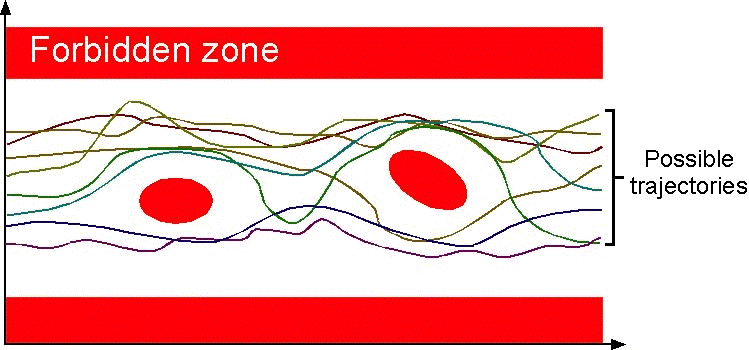
Safety properties of a program express that no possible execution of the program when considering all possible execution environments can reach an erroneous state. Graphically, the set of these erroneous states can be represented as a forbidden zone:
x(t)
t

4.  Proof of Safety Properties

The verification of safety properties consists in proving that the intersection of the concrete semantics of the program with the forbidden zone is empty. Since the program concrete semantics is not computable, the verification problem is undecidable. It is not always possible to answer the safety questions completely automatically, with finite computer resources, without any uncertainty about the answer and without any human intervention.

5.  Testing/Debugging

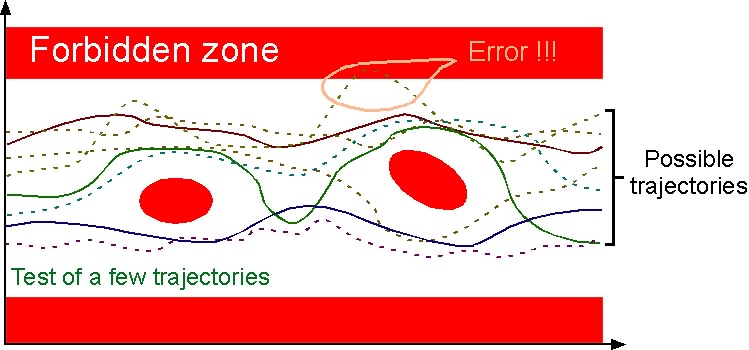
Testing/debugging consists in considering a subset of the possible executions:
x(t)
t

Testing/debugging is not a proof, since some erroneous trajectories might be forgotten. This is the problem of absence of coverage.

6.  Bounded model checking

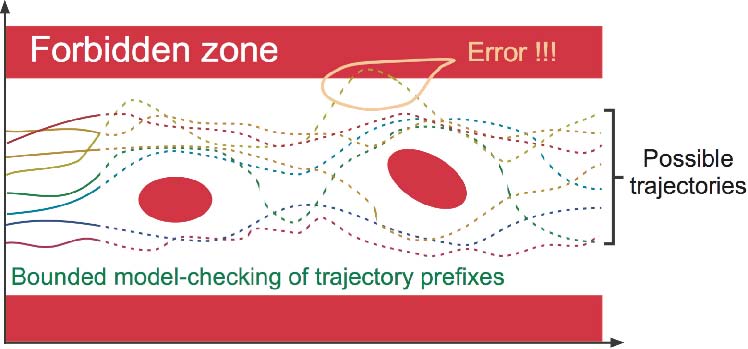
Bounded model checking consists in exploring the prefixes of the possible executions:
x(t)
t

Bounded model checking is not a proof, since late errors can be missed. This is the same problem of absence of coverage.

7.  Abstract Interpretation

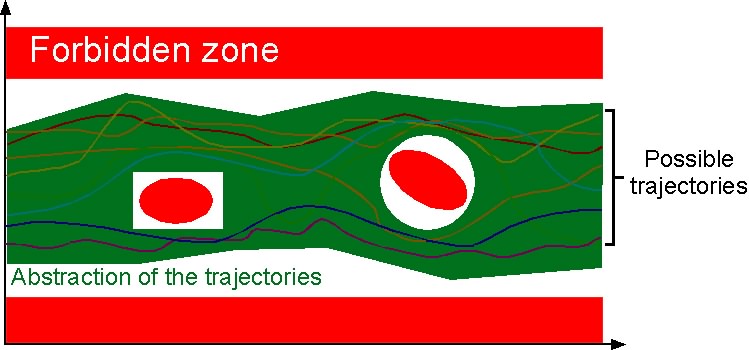
Abstract interpretation consists in considering an abstract semantics, that is a superset of the concrete program semantics:
x(t)
t

The abstract semantics covers all possible cases. Whence, if the abstract semantics is safe (i.e. does not intersect the forbidden zone) then so is the concrete semantics.

8.  Formal Methods

Formal methods are abstract interpretations which differ in the way the abstract semantics is obtained. In all cases, the abstract semantics must be chosen to be computer representable.

• In model-checking, the abstract semantics is provided manually by the user in the form of a finitary model of the program execution (for example a finite automaton) [9]. In some cases the model can be computed automatically, by methods relevant to static analysis.
• In deductive methods the abstract semantics is specified by verification conditions and must be provided by the user in the form of inductive properties (true at each program step, such as loop invariants) satisfying these verification conditions [5]. The inductive properties must be found manually by the user and the theorem prover sometimes needs assistance to prove that they are indeed inductive. To help the user in this discovery task, some of these inductive properties can be computed automatically, by techniques relevant to static analysis.
• In static analysis, the abstract semantics is computed automatically thanks to predefined approximations [1,6,7,8], possibly manually parameterizable by the user.

In all cases, the abstract semantics should be sound (section 1.8 ), remain sufficiently precise to avoid false alarms (section 1.10 ) while remaining as simple as possible to avoid combinatorial explosion phenomena (section 1.13 ).

9.  Erroneous Abstractions

In formal methods the abstract semantics must be chosen as a superset of the concrete semantics since otherwise reasonings in the abstract might not be correct in the concrete:
x(t)
t

We say that an abstraction is sound (or correct) if the abstract semantics covers all possible cases of the concrete semantics. All formal methods are required to use sound abstractions: if a potential error is not signaled that it should be definitely impossible. Contrary to testing/debugging formal methods provide full coverage.

10.  Examples of Erroneous Abstractions

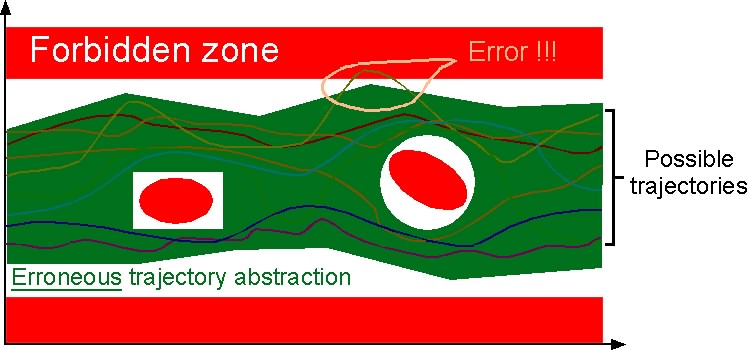
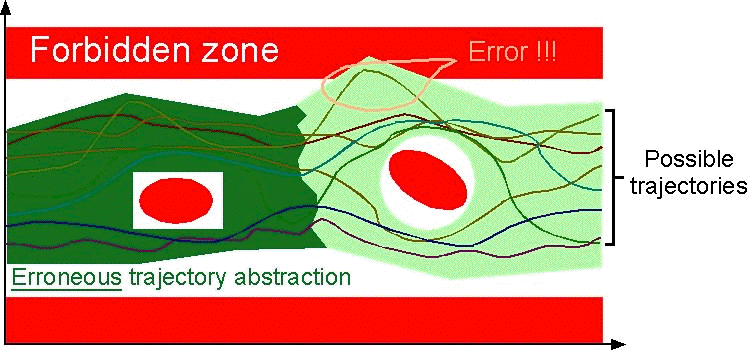
Yet, some methods, presented as formal, do not explore all possible trajectories, but only prefixes (such as the "bounded model-checking") or may not terminate (such as the "refinement model-checking") and therefore should be considered as incorrect, since some errors can be forgotten:
x(t)
t

11.  False Alarms

• correct/sound, that is a superset of the concrete semantics, and
• simple, or at least simple enough to be representable in a machine.

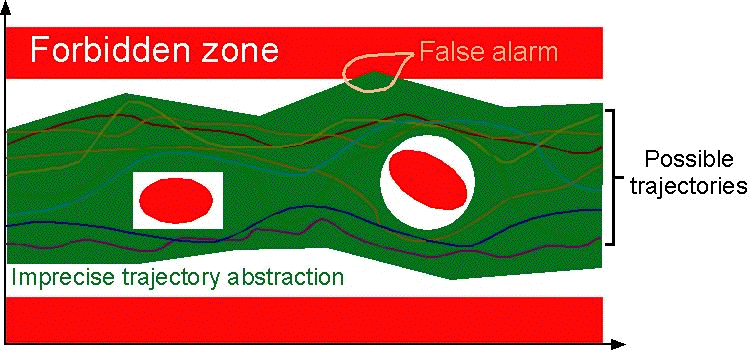
In absence of alarms, this yields a corectness proof. However, the consequence of the overapproximation of the possible executions is that inexisting executions are considered, some of which are erroneous, which leads to false alarms (also called false positives). A false alarm corresponds to the case when the abstract semantics intersects the forbidden zone while the concrete semantics does not intersect this forbidden zone. So a potential error is signaled which can never occur in reality:
x(t)
t

12.  Incompleteness of Formal Methods

Automatic formal methods are all incomplete: there exists an infinity of programs for which potential errors at execution are signaled, even if they are definitely impossible in reality.

• In model-checking an alarm in the model may not correspond to an inevitable error in the modelized system¹.
• In deductive methods, false alarms may be due to the impossibility to prove automatically that the user provided invariant is indeed inductive.
• In static analysis, false alarms are due to a lack of precision of the analysis.

Such false alarms are inevitable because all questions that formal methods try to solve are undecidable. Il will always be possible to find a program without any run-time error for which the abstract semantics will be too imprecise to prove the absence of error fully automatically, without any human intervention. The imprecision problem can often be solved by choosing a more refined abstract semantics, which is more precise and so often more complex, which results in larger computation costs.

13.  Excluded Miracle

In summary, with testing/debugging a subset of the possible program executions is considered, so that errors can be forgotten. With abstract interpretation-based formal methods, a superset of the possible program executions is considered, so that, because of the potential imprecision, one can invent errors that do not exist in reality (so called "false alarms").

Hence one would like to have correct formal methods (without erroneous abstractions by absence of coverage) and complete (without false alarms due to over-coverage). Such an abstraction does exists mathematically [4], but it is impossible to compute, and this because if undecidability, which amounts to say that it is impossible to execute the program in all possible execution environment in a finite time with a finite memory.

14.  Invariants

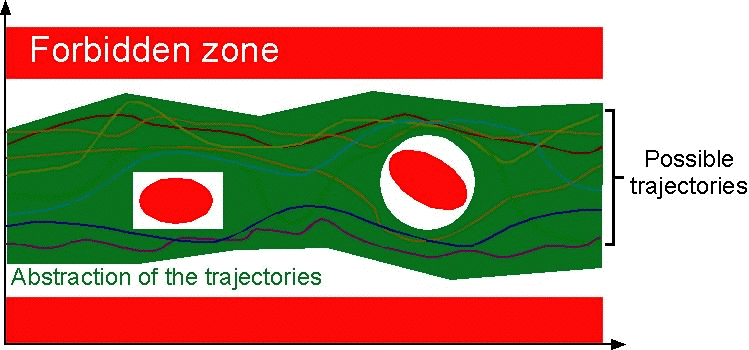
An invariant is a property which holds for all trajectories.

In the example below, a first invariant would be that all states reachable during the course of the computation can be on any trajectory. This is already an approximation since this leaves the possibility to jump from one trajectory to another, and even to go backwards.

A second invariant, less precise, would be that all trajectories are in the green zone . This is a less precise approximation which leaves the possibility to reach points out of any trajectory:
x(t)
t

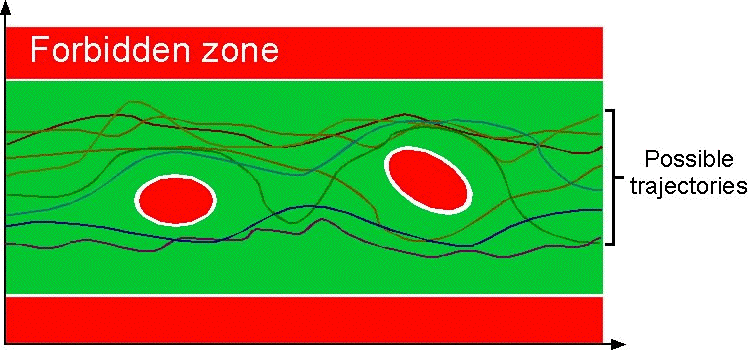
This second invariant imples a third one, even less precise, stating that all trajectories are outside the forbidden red zone :
x(t)
t

15.  Program Abstract Invariants

A program invariant is a program property which holds during the program execution. The ASTRÉE static analyzer computes automatically an abstract semantics which consists of local abstract invariants attached to program points or to program blocks stating properties about part of the program variables which are visible at that program point or withing that block. These local invariants holds of the involved variables whenever control reaches that program point or stays within that block.

16.  Abstract Domains

An abstract domain of the ASTRÉE static analyzer is a computer representation of a given category of invariants and of the operations involved in the computation of these abstract invariants. ASTRÉE uses a great number of abstract domains which are combined to obtain complex abstract invariants. The term "abstract" makes reference to the fact that the computed invariants are correct approximations of the program concrete semantics.

A classical abstract domain is that of intervals [2,6,8] which approximate an ordered set of values by their minimum and their maximum. Applied to our example, this interval abstraction yields the following invariant:
x(t)
t
which is too imprecise to prove the specification. To be precise, ASTRÉE incorporates abstract domains which are expressive enough to take into account the properties of command programs controlling complex discrete dynamical systems.

17.  More on abstract interrpetation

Bibliography

[1]

P. Cousot. Semantic foundations of program analysis. In S.S. Muchnick and N.D. Jones, editors, Program Flow Analysis: Theory and Applications, chapter 10, pages 303-342. PrenticeHall, 1981.

[2]

P. Cousot. Abstract interpretation based formal methods and future challenges, invited paper. In R. Wilhelm, editor, « Informatics - 10 Years Back, 10 Years Ahead », volume 2000 of LNCS, pages 138-156. Springer, 2000.

[3]

P. Cousot. Interprétation abstraite. TSI, 19(1-2-3):155-164, Jan. 2000.

[4]

P. Cousot. Partial completeness of abstract fixpoint checking, invited paper. In B.Y. Choueiry and T. Walsh, editors, Proc. 4^th Int. Symp. SARA '2000, Horseshoe Bay, TX, US, LNAI 1864, pages 1-25. Springer, 26-29 Jul. 2000.

[5]

P. Cousot. Constructive design of a hierarchy of semantics of a transition system by abstract interpretation. Theoret. Comput. Sci., 277(1-2):47-103, 2002.

[6]

P. Cousot and R. Cousot. Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In 4^th POPL, pages 238-252, Los Angeles, CA, 1977. ACM Press.

[7]

P. Cousot and R. Cousot. Systematic design of program analysis frameworks. In 6^th POPL, pages 269-282, San Antonio, TX, 1979. ACM Press.

[8]

P. Cousot and R. Cousot. Comparing the Galois connection and widening/narrowing approaches to abstract interpretation, invited paper. In M. Bruynooghe and M. Wirsing, editors, Proc. 4^th Int. Symp. PLILP '92, Leuven, BE, 26-28 Aug. 1992, LNCS 631, pages 269-295. Springer, 1992.

[9]

P. Cousot and R. Cousot. Temporal abstract interpretation. In 27^th POPL, pages 12-25, Boston, MA, Jan. 2000. ACM Press.

Online courses on abstract interpretation

Notes: