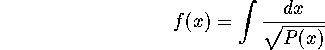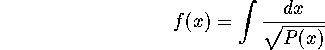Résolution des équations de degré 5
L'exposé de maîtrise suivant a été
présenté par Gaël Benabou et moi-même en mai
1998. Le sujet a été proposé par Yves Laszlo.
Le texte complet
ps.gz ou
pdf.
Résumé
Introduction
Il est bien connu que l'on peut résoudre les équations de degré
inférieur ou égal à quatre en utilisant les opérations
habituelles +, -, *, / et racine nième.
Cela est cependant impossible pour les équations de degré 5 ou
plus. On se propose donc de présenter une méthode de résolution
des équations de degré 5, en ajoutant aux opérations
précédentes une nouvelle classe de fonctions : des fonctions
elliptiques.
Équations de degré 3 et 4, théorie de Galois
Dans cette partie, on rappelle le résultat de Galois qui montre
l'irrésolubilité des équations de degré 5, et on présente la
méthode de résolution des équations de degré 3 et 4
(méthodes de Cardan et Lagrange). On retrouvera des points communs
pour le degré 5 : division des périodes, fonction prenant peu de
valeurs par permutation des racines du polynôme...
Fonctions elliptiques
Ici, on décrit les fonctions elliptiques comme généralisation
des fonctions exponentielle et logarithme. On considère en effet les
fonctions de C dans C de la forme suivante, ainsi que leurs
réciproques :
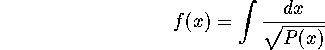
où P est un polynôme.
On explique ensuite le lien entre fonctions elliptiques et fonctions
doublement périodiques. Ensuite, le fait que ces fonctions soient
méromorphes permet d'obtenir un certain nombre de relations, qui
permettront dans la partie suivante de résoudre une certaine classe
d'équations de degré 6.
Méthode de résolution de l'équation générale de degré 5
On peut alors exposer les étapes de la résolution d'une équation
générale de degré cinq. L'idée est de se ramener progressivement à des
équations de plus en plus simples (même si la dernière est de degré 6, elle
est suffisamment particulière pour qu'on sache la résoudre).
Équation générale
X5 + A X4 + B X3 + C X2 + D X + E = 0
|
Transformation de Tschirnhausen
|
Équation principale
z5 + 5 a z2 + 5 b z + c = 0
|
Polynômes de polyèdres
|
Équation de Brioschi
y5 - 10 Z y3 + 45 Z2 y - Z2 = 0
|
Théorème de Perron
|
Équation de Jacobi
s6 + (10/a) s3 - 12 (g2/a2) s + 5 /
a2 = 0
|
Fonctions de Weierstrass - Evaluation de périodes
La transformation de Tschirnhausen consiste grosso modo à effectuer
un changement de variable permettant de réduire le nombre de
coefficients qui interviennent dans l'équation.
Ensuite, l'utilisation des polynômes de polyèdres (qui utilise les
propriétés de l'icosaèdre régulier, i.e. le polyèdre
régulier à 20 faces) permet de se ramener à une autre
forme d'équation de degré 5.
Enfin, le théorème de Perron, qui utilise encore des
propriétés de l'icosaèdre, nous donne exactement l'équation de
degré 6 que l'on sait résoudre à l'aide des fonctions
elliptiques.
Retour à la page principale