Paper

M. Cho, K. Alahari, J. Ponce
Learning Graphs to Match
Proceedings of the IEEE Interational Conference on Computer Vision (2013)
PDF |
Abstract |
BibTeX |
Slides PDF(38MB) |
Slides PPTX(68MB)
Abstract
Many tasks in computer vision are formulated as graph
matching problems. Despite the NP-hard nature of the
problem, fast and accurate approximations have led to significant
progress in a wide range of applications. Learning
graph models from observed data, however, still remains a
challenging issue. This paper presents an effective scheme
to parameterize a graph model, and learn its structural attributes
for visual object matching. For this, we propose a
graph representation with histogram-based attributes, and
optimize them to increase the matching accuracy. Experimental
evaluations on synthetic and real image datasets
demonstrate the effectiveness of our approach, and show
significant improvement in matching accuracy over graphs
with pre-defined structures.
BibTeX
@InProceedings{cho2013,
author = {Minsu Cho and Karteek Alahari and Jean Ponce},
title = {Learning Graphs to Match},
booktitle = {Proceedings of the IEEE Interational Conference on Computer Vision},
year = {2013}
}
Dataset

Code

Overview
The goal of this work is to learn a class-specific graph model for matching problems.
Graph matching is widely used in many computer vision problems, and
much progress has been achieved recently in various applications of graph matching,
such as shape analysis, image matching, action recognition, and object categorization.
For many tasks, however, a natural question arises: How can we obtain a good graph model
for a target object to match? Recent studies have revealed that simple graphs with
hand-crafted structures and similarity functions, typically used in graph matching,
are insufficient to capture the inherent structure underlying the problem at hand.
As a consequence, a better optimization of the graph matching objective does not guarantee
better correspondence accuracy. Previous learning methods for graph matching tackle this issue
by learning a set of parameters in the objective function [Caetano et al. 2009, Leordeanu et al. 2012].
Although it is useful to learn such a matching function for two graphs of a certain class,
a more apt goal would be to learn a graph model to match, which provides an optimal matching
to all instances of the class. Such a learned graph would better model the inherent structure
in the target class, thus resulting in better performance for matching.
Figure 1 illustrates the difference between the previous approaches and ours.
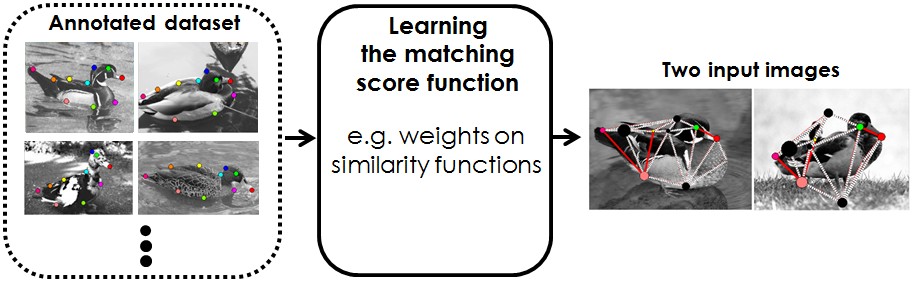 | 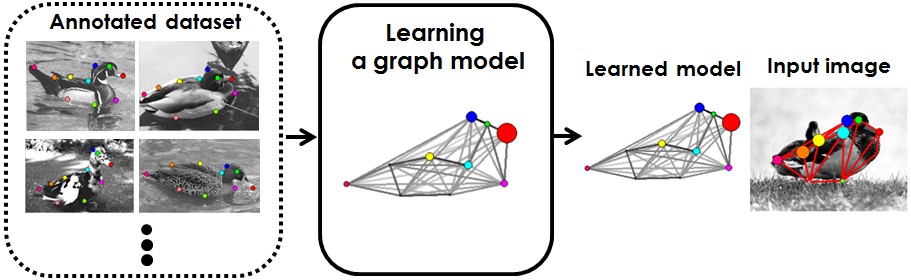 |
| (a) Learning graph matching | (b) Learning a class-specific graph model for matching |
Figure 1. Comparison between the previous approaches and the proposed model learning.
To this end, we present a generalized formulation
for graph matching, which is an extension of the previous learning approaches,
and propose to learn a graph model based
on a particular, yet rather general, graph representation with histogram-based attributes
for nodes and edges.
We show that all attributes of such a graph can be learned in a structued-output max-margin framework
[Tsochantaridis at el. 2005].
The proposed method reconstructs a graph model inherent in a target class,
and provides significant improvement in matching performance, as demonstrated in our experiments
on synthetic and real datasets.
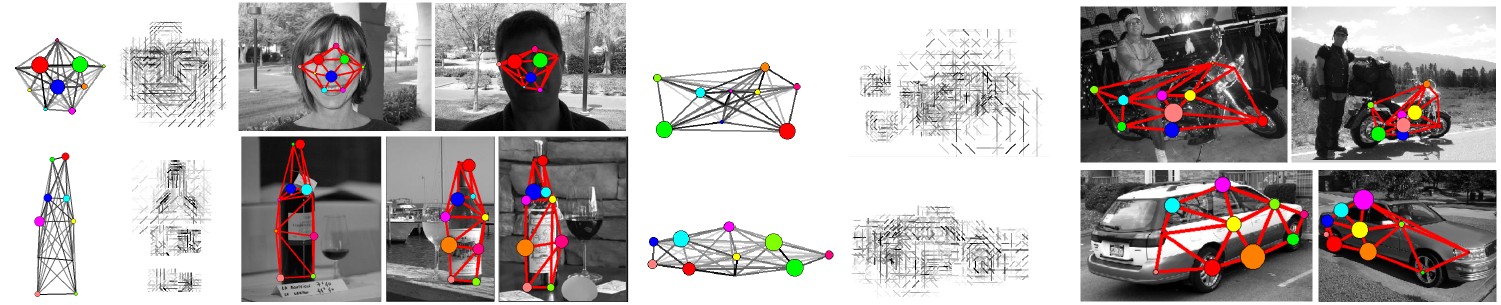
Figure 2. Learned graph models and their matching results.
Figure 2 above shows the learned graph models on object classes, and their matching examples.
For each class, the learned graph model, its learned appearance in node attributes,
and matching results are shown. In the graph model, bigger circles represent stronger nodes,
and darker lines denote stronger edges. In the second and the fifth columns,
to better visualize node attributes, we show the edge responses based on the learned SIFT attributes.
For each model, some matching examples with high scores are shown.
The results show that the learned graph model enables robust matching in spite of
deformation and appearance changes.
Acknowledgements
This research was supported in part by the ERC advanced
grant VideoWorld, Institut Universitaire de France, and the
Quaero programme funded by the OSEO.